The HPPLS Procedure
Example 12.1 Choosing a PLS Model by Test Set Validation
This example demonstrates issues in spectrometric calibration. The data (Umetrics 1995) consist of spectrographic readings on 33 samples that contain known concentrations of two amino acids, tyrosine and tryptophan.
The spectra are measured at 30 frequencies across the overall range of frequencies. For example, Output 12.1.1 shows the observed spectra for three samples: one with only tryptophan, one with only tyrosine, and one with a mixture of
the two, all at a total concentration of 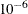 .
.
Output 12.1.1: Spectra for Three Samples of Tyrosine and Tryptophan
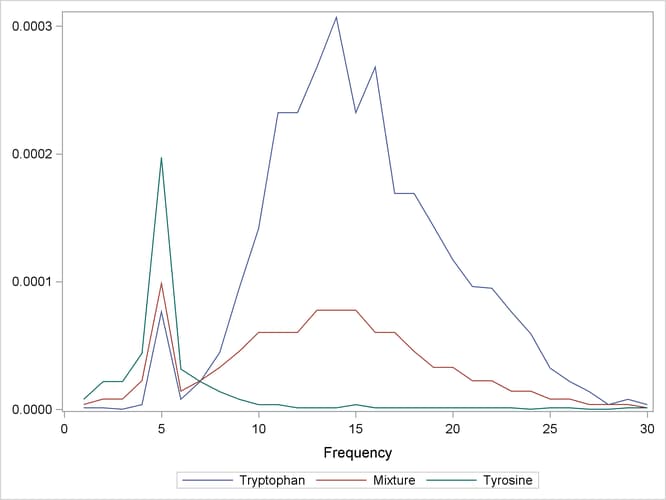
Of the 33 samples, 18 are used as a training set and 15 as a test set. The data originally appear in McAvoy et al. (1989).
These data were created in a lab, where the concentrations are fixed in order to provide a wide range of applicability for
the model. You want to use a linear function of the logarithms of the spectra to predict the logarithms of tyrosine and tryptophan
concentration, in addition to the logarithm of the total concentration. Actually, because zeros are possible in both the responses
and the predictors, slightly different transformations are used. The following statements create a SAS data set named ex1Data for these data. The data set also contains a variable Role that is used to assign samples to the training and testing roles.
data ex1Data; input obsnam $ Role : $5. tot tyr f1-f30 @@; try = tot - tyr; if (tyr) then tyr_log = log10(tyr); else tyr_log = -8; if (try) then try_log = log10(try); else try_log = -8; tot_log = log10(tot); datalines; 17mix35 TRAIN 0.00003 0 -6.215 -5.809 -5.114 -3.963 -2.897 -2.269 -1.675 -1.235 -0.900 -0.659 -0.497 -0.395 -0.335 -0.315 -0.333 -0.377 -0.453 -0.549 -0.658 -0.797 -0.878 -0.954 -1.060 -1.266 -1.520 -1.804 -2.044 -2.269 -2.496 -2.714 19mix35 TRAIN 0.00003 3E-7 -5.516 -5.294 -4.823 -3.858 -2.827 -2.249 -1.683 -1.218 -0.907 -0.658 -0.501 -0.400 -0.345 -0.323 -0.342 -0.387 -0.461 -0.554 -0.665 -0.803 -0.887 -0.960 -1.072 -1.272 -1.541 -1.814 -2.058 -2.289 -2.496 -2.712 21mix35 TRAIN 0.00003 7.5E-7 -5.519 -5.294 -4.501 -3.863 -2.827 -2.280 -1.716 -1.262 -0.939 -0.694 -0.536 -0.444 -0.384 -0.369 -0.377 -0.421 -0.495 -0.596 -0.706 -0.824 -0.917 -0.988 -1.103 -1.294 -1.565 -1.841 -2.084 -2.320 -2.521 -2.729 23mix35 TRAIN 0.00003 1.5E-6 ... more lines ... 26tyro5 TEST 0.00001 0.00001 -3.037 -2.696 -2.464 -2.321 -2.239 -2.444 -2.602 -2.823 -3.144 -3.396 -3.742 -4.063 -4.398 -4.699 -4.893 -5.138 -5.140 -5.461 -5.463 -5.945 -5.461 -5.138 -5.140 -5.138 -5.138 -5.463 -5.461 -5.461 -5.461 -5.461 tyro2 TEST 0.0001 0.0001 -1.081 -0.710 -0.470 -0.337 -0.327 -0.433 -0.602 -0.841 -1.119 -1.423 -1.750 -2.121 -2.449 -2.818 -3.110 -3.467 -3.781 -4.029 -4.241 -4.366 -4.501 -4.366 -4.501 -4.501 -4.668 -4.668 -4.865 -4.865 -5.109 -5.111 ;
The following statements fit a PLS model that has 10 factors.
proc hppls data=ex1Data nfac=10; model tot_log tyr_log try_log = f1-f30; run;
The "Model Information" table in Output 12.1.2 shows that no validation method is used. The "Number of Observations" table confirms that all 33 sample observations are used in the analysis.
The table in Output 12.1.3 indicates that only four or five factors are required to explain almost all of the variation in both the predictors and the responses.
Output 12.1.2: Model Information and Number of Observations
Output 12.1.3: Amount of Variation Explained
| Percent Variation Accounted for by Partial Least Squares Factors | ||||
|---|---|---|---|---|
| Number of Extracted Factors |
Model Effects | Dependent Variables | ||
| Current | Total | Current | Total | |
| 1 | 77.67903 | 77.67903 | 47.80217 | 47.80217 |
| 2 | 20.62719 | 98.30622 | 38.96826 | 86.77043 |
| 3 | 1.00143 | 99.30766 | 6.89262 | 93.66305 |
| 4 | 0.24930 | 99.55696 | 1.77222 | 95.43528 |
| 5 | 0.13077 | 99.68773 | 1.71762 | 97.15290 |
| 6 | 0.08970 | 99.77742 | 0.58619 | 97.73909 |
| 7 | 0.05684 | 99.83426 | 0.29079 | 98.02988 |
| 8 | 0.06730 | 99.90156 | 0.13857 | 98.16845 |
| 9 | 0.01521 | 99.91676 | 0.68214 | 98.85059 |
| 10 | 0.02627 | 99.94304 | 0.14388 | 98.99447 |
In order to choose the optimal number of PLS factors, you can explore how well models that are based on data in training roles
and have different numbers of factors fit the data in testing roles. To do so, you can use the PARTITION
statement to assign observations to training and testing roles based on the values of the input variable named Role.
proc hppls data=ex1Data nfac=10 cvtest(stat=press seed=12345); model tot_log tyr_log try_log = f1-f30; partition roleVar = Role(train='TRAIN' test='TEST'); run;
Output 12.1.4 shows the "Model Information" table and the "Number of Observations" table. The "Model Information" table indicates that test set validation is used and displays information about the options that are used in the model comparison test. The "Number of Observations" table confirms that there are 18 observations for the training role and 15 for the testing role.
Output 12.1.5 displays the results of the test set validation. They indicate that although five PLS factors produce the minimum predicted residual sum of squares, the residuals for four factors are insignificantly different from the residuals for five factors. Thus, the smaller model is preferred.
Output 12.1.4: Model Information and Number of Observations with Test Set Validation
Output 12.1.5: Test Set Validation for the Number of PLS Factors
| Test Set Validation for the Number of Extracted Factors |
||
|---|---|---|
| Number of Extracted Factors |
Root Mean PRESS |
Prob > PRESS |
| 0 | 3.056797 | <.0001 |
| 1 | 2.630561 | <.0001 |
| 2 | 1.00706 | 0.0070 |
| 3 | 0.664603 | <.0001 |
| 4 | 0.521578 | 0.3760 |
| 5 | 0.500034 | 1.0000 |
| 6 | 0.513561 | 0.5000 |
| 7 | 0.501431 | 0.6850 |
| 8 | 1.055791 | 0.1520 |
| 9 | 1.435085 | 0.1010 |
| 10 | 1.720389 | 0.0330 |
| Percent Variation Accounted for by Partial Least Squares Factors | ||||
|---|---|---|---|---|
| Number of Extracted Factors |
Model Effects | Dependent Variables | ||
| Current | Total | Current | Total | |
| 1 | 81.16545 | 81.16545 | 48.33854 | 48.33854 |
| 2 | 16.81131 | 97.97676 | 32.54654 | 80.88508 |
| 3 | 1.76391 | 99.74067 | 11.44380 | 92.32888 |
| 4 | 0.19507 | 99.93574 | 3.83631 | 96.16519 |
