The HPLMIXED Procedure

Statistical Properties

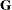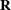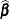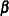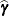If $\bG $ and $\bR $ are known, $\widehat{\bbeta }$ is the best linear unbiased estimator (BLUE) of $\bbeta $, and $\widehat{\bgamma }$ is the best linear unbiased predictor (BLUP) of 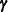$\bgamma $ (Searle 1971; Harville 1988, 1990; Robinson 1991; McLean, Sanders, and Stroup 1991). Here, "best" means minimum mean squared error. The covariance matrix of 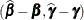$(\widehat{\bbeta } - \bbeta ,\widehat{\bgamma } - \bgamma )$ is

\[ \mb{C} = \left[\begin{array}{cc} \mb{X}’\mb{R}^{-1}\mb{X} & \mb{X}’\mb{R}^{-1}\mb{Z} \\*\mb{Z}’\mb{R}^{-1}\mb{X} & \mb{Z}’\mb{R}^{-1}\mb{Z} + \mb{G}^{-1} \end{array}\right]^{-} \]

where $^-$ denotes a generalized inverse ( Searle 1971).

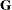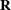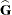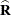However, $\bG $ and $\bR $ are usually unknown and are estimated by using one of the aforementioned methods. These estimates, $\widehat{\bG }$ and $\widehat{\bR }$, are therefore simply substituted into the preceding expression to obtain

\[ \widehat{\mb{C}} = \left[\begin{array}{cc} \bX ’\widehat{\bR }^{-1}\bX & \bX ’\widehat{\bR }^{-1}\bZ \\*\bZ ’\widehat{\bR }^{-1}\bX & \bZ ’\widehat{\bR }^{-1}\bZ + \widehat{\bG }^{-1} \end{array}\right]^{-} \]

as the approximate variance-covariance matrix of 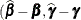$(\widehat{\bbeta } - \bbeta ,\widehat{\bgamma } - \bgamma $). In this case, the BLUE and BLUP acronyms no longer apply, but the word empirical is often added to indicate such an approximation. The appropriate acronyms thus become EBLUE and EBLUP.

McLean and Sanders (1988) show that 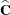$\widehat{\bC }$ can also be written as

\[ \widehat{\bC } = \left[\begin{array}{cc} \widehat{\bC }_{11} & \widehat{\bC }_{21}’ \\ \widehat{\bC }_{21} & \widehat{\bC }_{22} \end{array}\right] \]

where

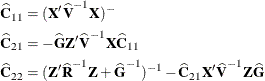
\begin{align*} \widehat{\bC }_{11} & = (\bX ’\widehat{\bV }^{-1}\bX )^{-} \\ \widehat{\bC }_{21} & = -\widehat{\bG }\bZ ’\widehat{\bV }^{-1}\bX \widehat{\bC }_{11} \\ \widehat{\bC }_{22} & = (\bZ ’\widehat{\bR }^{-1}\bZ + \widehat{\bG }^{-1})^{-1} - \widehat{\bC }_{21}\bX ’\widehat{\bV }^{-1}\bZ \widehat{\bG } \end{align*}

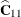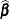Note that $\widehat{\bC }_{11}$ is the familiar estimated generalized least squares formula for the variance-covariance matrix of $\widehat{\bbeta }$.