The HPLMIXED Procedure

Notation for the Mixed Model

This section introduces the mathematical notation used throughout this chapter to describe the mixed linear model and assumes familiarity with basic matrix algebra (for an overview, see Searle 1982). A more detailed description of the mixed model is contained in the section Linear Mixed Models Theory.

A statistical model is a mathematical description of how data are generated. The standard linear model, as used by the GLM procedure, is one of the most common statistical models:

\[ \mb{y} = \mb{X}\bbeta + \bepsilon \]

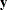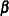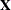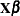In this expression, $\mb{y}$ represents a vector of observed data, $\bbeta $ is an unknown vector of fixed-effects parameters with a known design matrix $\mb{X}$, and $\bepsilon $ is an unknown random error vector that models the statistical noise around $\mb{X}\bbeta $. The focus of the standard linear model is to model the mean of 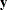$\mb{y}$ by using the fixed-effects parameters 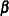$\bbeta $. 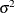The residual errors $\bepsilon $ are assumed to be independent and identically distributed Gaussian random variables with mean 0 and variance $\sigma ^2$.

The mixed model generalizes the standard linear model as follows:

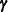\[ \mb{y} = \mb{X}\bbeta + \mb{Z}\bgamma + \bepsilon \]

Here, $\bgamma $ is an unknown vector of random-effects parameters with a known design matrix 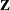$\mb{Z}$, and $\bepsilon $ is an unknown random error vector whose elements are no longer required to be independent and homogeneous.

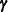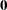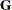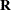To further develop this notion of variance modeling, assume that $\bgamma $ and $\bepsilon $ are Gaussian random variables that are uncorrelated, have expectations $\mb{0}$, and have variances $\mb{G}$ and $\mb{R}$, respectively. The variance of 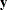$\mb{y}$ is thus

\[ \mb{V} = \mb{ZGZ} ’ + \mb{R} \]

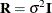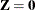Note that when $\mb{R} = \sigma ^2\mb{I}$ and $\mb{Z} = \mb{0}$, the mixed model reduces to the standard linear model.

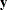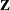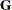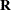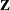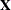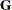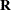You can model the variance of the data $\mb{y}$ by specifying the structure of $\mb{Z}$, $\mb{G}$, and $\mb{R}$. The model matrix $\mb{Z}$ is set up in the same fashion as $\mb{X}$, the model matrix for the fixed-effects parameters. For $\mb{G}$ and $\mb{R}$, you must select some covariance structure. Possible covariance structures include the following:

  • variance components

  • compound symmetry (common covariance plus diagonal)

  • unstructured (general covariance)

  • autoregressive

  • spatial

  • general linear

  • factor analytic

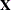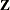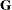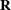By appropriately defining the model matrices $\bX $ and $\bZ $ in addition to the covariance structure matrices $\bG $ and $\bR $, you can perform numerous mixed model analyses.