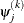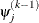The HPLMIXED Procedure
PROC HPLMIXED Statement
-
PROC HPLMIXED <options>;
The PROC HPLMIXED statement invokes the procedure. Table 9.2 summarizes important options in the PROC HPLMIXED statement by function. These and other options in the PROC HPLMIXED statement are then described fully in alphabetical order.
Table 9.2: PROC HPLMIXED Statement Options
|
Option |
Description |
|---|---|
|
Basic Options |
|
|
Specifies the input data set |
|
|
Specifies the estimation method |
|
|
Limits the length of effect names |
|
|
Computes the best linear unbiased prediction |
|
|
Options Related to Output |
|
|
Suppresses the "Class Level Information" table completely or in parts |
|
|
Specifies the maximum levels of CLASS variables to print |
|
|
Displays the rank of design matrix |
|
|
Optimization Options |
|
|
Tunes an absolute function convergence criterion |
|
|
Tunes an absolute function difference convergence criterion |
|
|
Tunes the absolute gradient convergence criterion |
|
|
Tunes the relative function convergence criterion |
|
|
Tunes the relative gradient convergence criterion |
|
|
Chooses the maximum number of iterations in any optimization |
|
|
Specifies the maximum number of function evaluations in any optimization |
|
|
Specifies the upper limit on seconds of CPU time for any optimization |
|
|
Specifies the minimum number of iterations in any optimization |
|
|
Selects the optimization technique |
|
|
Tunes the relative parameter convergence criterion |
|
You can specify the following options in the PROC HPLMIXED statement.

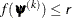
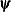
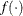
![\[ |f(\bpsi ^{(k-1)}) - f(\bpsi ^{(k)})| \leq \Argument{r} \]](images/stathpug_hplmixed0025.png)
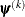
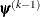
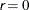
![\[ \max _ j |g_ j(\bpsi ^{(k)})| \leq \Argument{r} \]](images/stathpug_hplmixed0029.png)
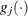
![\[ \frac{|f(\bpsi ^{(k)}) - f(\bpsi ^{(k-1)})|}{|f(\bpsi ^{(k-1)})|} \leq \Argument{r} \]](images/stathpug_hplmixed0031.png)
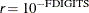
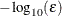

![\[ \frac{\mb{g}(\bpsi ^{(k)})^\prime [\bH ^{(k)}]^{-1} \mb{g}(\bpsi ^{(k)})}{|f(\bpsi ^{(k)})| } \leq \Argument{r} \]](images/stathpug_hplmixed0035.png)
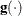
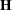
![\[ \frac{\parallel \mb{g}(\bpsi ^{(k)}) \parallel _2^2 \quad \parallel \mb{s}(\bpsi ^{(k)}) \parallel _2}{\parallel \mb{g}(\bpsi ^{(k)}) - \mb{g}(\bpsi ^{(k-1)}) \parallel _2 |f(\bpsi ^{(k)})| } \leq \Argument{r} \]](images/stathpug_hplmixed0038.png)


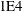
![\[ \frac{\max _ j |\psi _ j^{(k)} - \psi _ j^{(k-1)}| }{\max (|\psi _ j^{(k)}|,|\psi _ j^{(k-1)}|)} \leq \Argument{r} \]](images/stathpug_hplmixed0042.png)