The HPLMIXED Procedure
Formulation of the Mixed Model
The previous general linear model is certainly a useful one (Searle 1971), and it is the one fitted by the GLM procedure. However, many times the distributional assumption about  is too restrictive. The mixed model extends the general linear model by allowing a more flexible specification of the covariance
matrix of
is too restrictive. The mixed model extends the general linear model by allowing a more flexible specification of the covariance
matrix of  . In other words, it allows for both correlation and heterogeneous variances, although you still assume normality.
. In other words, it allows for both correlation and heterogeneous variances, although you still assume normality.
![\[ \mb{y} = \mb{X}\bbeta + \mb{Z}\bgamma +\bepsilon \]](images/stathpug_hplmixed0161.png)
where everything is the same as in the general linear model except for the addition of the known design matrix, 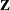 , and the vector of unknown random-effects parameters,
, and the vector of unknown random-effects parameters, 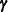 . The matrix
. The matrix 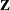 can contain either continuous or dummy variables, just like
can contain either continuous or dummy variables, just like 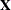 . The name mixed model comes from the fact that the model contains both fixed-effects parameters,
. The name mixed model comes from the fact that the model contains both fixed-effects parameters, 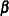 , and random-effects parameters,
, and random-effects parameters, 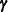 . See Henderson (1990) and Searle, Casella, and McCulloch (1992) for historical developments of the mixed model.
. See Henderson (1990) and Searle, Casella, and McCulloch (1992) for historical developments of the mixed model.
A key assumption in the foregoing analysis is that 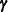 and
and  are normally distributed with
are normally distributed with
![\begin{align*} \mr{E}\left[ \begin{array}{c} \bgamma \\ \bepsilon \end{array} \right] & = \left[\begin{array}{c} \Strong{0} \\ \Strong{0} \end{array} \right] \\ \mr{Var}\left[ \begin{array}{c} \bgamma \\ \bepsilon \end{array} \right] & = \left[\begin{array}{cc} \mb{G} & \Strong{0} \\ \Strong{0} & \mb{R} \end{array} \right] \end{align*}](images/stathpug_hplmixed0162.png)
Therefore, the variance of 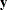 is
is 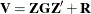 . You can model
. You can model 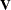 by setting up the random-effects design matrix
by setting up the random-effects design matrix 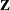 and by specifying covariance structures for
and by specifying covariance structures for 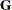 and
and 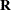 .
.
Note that this is a general specification of the mixed model, in contrast to many texts and articles that discuss only simple
random effects. Simple random effects are a special case of the general specification with 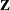 containing dummy variables,
containing dummy variables, 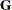 containing variance components in a diagonal structure, and
containing variance components in a diagonal structure, and 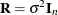 , where
, where 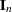 denotes the
denotes the 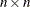 identity matrix. The general linear model is a further special case with
identity matrix. The general linear model is a further special case with 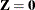 and
and 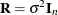 .
.
The following two examples illustrate the most common formulations of the general linear mixed model.
Example: Growth Curve with Compound Symmetry
Suppose that you have three growth curve measurements for s individuals and that you want to fit an overall linear trend in time. Your 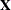 matrix is as follows:
matrix is as follows:
![\[ \mb{X} = \left[ \begin{array}{rr} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ \vdots & \vdots \\ 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ \end{array} \right] \]](images/stathpug_hplmixed0169.png)
The first column (coded entirely with 1s) fits an intercept, and the second column (coded with series of 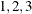 ) fits a slope. Here,
) fits a slope. Here, 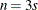 and
and 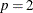 .
.
Suppose further that you want to introduce a common correlation among the observations from a single individual, with correlation
being the same for all individuals. One way of setting this up in the general mixed model is to eliminate the 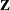 and
and 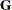 matrices and let the
matrices and let the 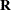 matrix be block-diagonal with blocks corresponding to the individuals and with each block having the compound-symmetry structure. This structure has two unknown parameters, one modeling a common covariance and the other modeling a residual
variance. The form for
matrix be block-diagonal with blocks corresponding to the individuals and with each block having the compound-symmetry structure. This structure has two unknown parameters, one modeling a common covariance and the other modeling a residual
variance. The form for 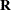 would then be
would then be
![\[ \mb{R} = \left[ \begin{array}{ccccccc} \sigma ^2_1 + \sigma ^2 & \sigma ^2_1 & \sigma ^2_1 & & & & \\ \sigma ^2_1 & \sigma ^2_1 + \sigma ^2 & \sigma ^2_1 & & & & \\ \sigma ^2_1 & \sigma ^2_1 & \sigma ^2_1 + \sigma ^2 & & & & \\ & & & \ddots & & & \\ & & & & \sigma ^2_1 + \sigma ^2 & \sigma ^2_1 & \sigma ^2_1 \\ & & & & \sigma ^2_1 & \sigma ^2_1 + \sigma ^2 & \sigma ^2_1 \\ & & & & \sigma ^2_1 & \sigma ^2_1 & \sigma ^2_1 + \sigma ^2 \\ \end{array} \right] \]](images/stathpug_hplmixed0173.png)
where blanks denote zeros. There are 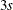 rows and columns altogether, and the common correlation is
rows and columns altogether, and the common correlation is 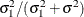 .
.
The following PROC HPLMIXED statements fit this model:
proc hplmixed; class indiv; model y = time; repeated morder/ type=cs subject=indiv; run;
Here, INDIV is a classification variable that indexes individuals. The MODEL
statement fits a straight line for TIME ; the intercept is fit by default just as in PROC GLM. The REPEATED
statement models the 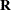 matrix: TYPE=CS
specifies the compound symmetry structure, and SUBJECT=
INDIV specifies the blocks of
matrix: TYPE=CS
specifies the compound symmetry structure, and SUBJECT=
INDIV specifies the blocks of 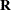 , and MORDER is the repeated effect that records the order of the measurements for each individual.
, and MORDER is the repeated effect that records the order of the measurements for each individual.
An alternative way of specifying the common intra-individual correlation is to let
![\begin{align*} \mb{Z} & = \left[ \begin{array}{cccc} 1 & & & \\ 1 & & & \\ 1 & & & \\ & 1 & & \\ & 1 & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \\ & & & 1 \\ & & & 1 \\ \end{array} \right] \\ \mb{G} & = \left[ \begin{array}{cccc} \sigma ^2_1 & & & \\ & \sigma ^2_1 & & \\ & & \ddots & \\ & & & \sigma ^2_1 \\ \end{array} \right] \end{align*}](images/stathpug_hplmixed0176.png)
and 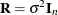 . The
. The 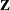 matrix has
matrix has 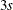 rows and s columns, and
rows and s columns, and 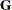 is
is  .
.
You can set up this model in PROC HPLMIXED in two different but equivalent ways:
proc hplmixed; class indiv; model y = time; random indiv; run; proc hplmixed; class indiv; model y = time; random intercept / subject=indiv; run;
Both of these specifications fit the same model as the previous one that used the REPEATED statement. However, the RANDOM specifications constrain the correlation to be positive, whereas the REPEATED specification leaves the correlation unconstrained.
Example: Split-Plot Design
The split-plot design involves two experimental treatment factors, A and B, and two different sizes of experimental units to which they are applied (Winer 1971; Snedecor and Cochran 1980; Milliken and Johnson 1992; Steel, Torrie, and Dickey 1997). The levels of A are randomly assigned to the larger-sized experimental units, called whole plots, whereas the levels of B are assigned to the smaller-sized experimental units, the subplots. The subplots are assumed to be nested within the whole plots, so that a whole plot consists of a cluster of subplots and
a level of A is applied to the entire cluster.
Such an arrangement is often necessary by nature of the experiment; the classical example is the application of fertilizer
to large plots of land and different crop varieties planted in subdivisions of the large plots. For this example, fertilizer
is the whole-plot factor A and variety is the subplot factor B.
The first example is a split-plot design for which the whole plots are arranged in a randomized block design. The appropriate PROC HPLMIXED statements are as follows:
proc hplmixed; class a b block; model y = a b a*b; random block a*block; run;
Here
![\[ \bR = \sigma ^2 \mb{I} _{24} \]](images/stathpug_hplmixed0178.png)
and 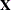 ,
, 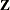 , and
, and 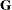 have the following form:
have the following form:
![\[ \bX = \left[ \begin{array}{cccccccccccc} 1 & 1 & & & 1 & & 1 & & & & & \\ 1 & 1 & & & & 1 & & 1 & & & & \\ 1 & & 1 & & 1 & & & & 1 & & & \\ 1 & & 1 & & & 1 & & & & 1 & & \\ 1 & & & 1 & 1 & & & & & & 1 & \\ 1 & & & 1 & & 1 & & & & & & 1 \\ \vdots & & \vdots & & \vdots & & & & & \vdots \\ 1 & 1 & & & 1 & & 1 & & & & & \\ 1 & 1 & & & & 1 & & 1 & & & & \\ 1 & & 1 & & 1 & & & & 1 & & & \\ 1 & & 1 & & & 1 & & & & 1 & & \\ 1 & & & 1 & 1 & & & & & & 1 & \\ 1 & & & 1 & & 1 & & & & & & 1 \\ \end{array} \right] \\ \]](images/stathpug_hplmixed0179.png)
![\[ \bZ \, = \left[ \begin{array}{cccccccccccccccc} 1 & & & & 1 & & & & & & & & & & & \\ 1 & & & & 1 & & & & & & & & & & & \\ 1 & & & & & 1 & & & & & & & & & & \\ 1 & & & & & 1 & & & & & & & & & & \\ 1 & & & & & & 1 & & & & & & & & & \\ 1 & & & & & & 1 & & & & & & & & & \\ & 1 & & & & & & 1 & & & & & & & & \\ & 1 & & & & & & 1 & & & & & & & & \\ & 1 & & & & & & & 1 & & & & & & & \\ & 1 & & & & & & & 1 & & & & & & & \\ & 1 & & & & & & & & 1 & & & & & & \\ & 1 & & & & & & & & 1 & & & & & & \\ & & 1 & & & & & & & & 1 & & & & & \\ & & 1 & & & & & & & & 1 & & & & & \\ & & 1 & & & & & & & & & 1 & & & & \\ & & 1 & & & & & & & & & 1 & & & & \\ & & 1 & & & & & & & & & & 1 & & & \\ & & 1 & & & & & & & & & & 1 & & & \\ & & & 1 & & & & & & & & & & 1 & & \\ & & & 1 & & & & & & & & & & 1 & & \\ & & & 1 & & & & & & & & & & & 1 & \\ & & & 1 & & & & & & & & & & & 1 & \\ & & & 1 & & & & & & & & & & & & 1 \\ & & & 1 & & & & & & & & & & & & 1 \\ \end{array} \right] \\ \]](images/stathpug_hplmixed0180.png)
![\[ \bG = \left[ \begin{array}{ccccccccc} \sigma ^2_ B & & & & & & & \\ & \sigma ^2_ B & & & & & & \\ & & \sigma ^2_ B & & & & & \\ & & & \sigma ^2_ B & & & & \\ & & & & \sigma ^2_{AB} & & & \\ & & & & & \sigma ^2_{AB} & & \\ & & & & & & \ddots & \\ & & & & & & & \sigma ^2_{AB} \\ \end{array} \right] \]](images/stathpug_hplmixed0181.png)
where 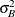 is the variance component for
is the variance component for Block and 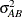 is the variance component for
is the variance component for A*Block. Changing the RANDOM
statement as follows fits the same model, but with 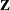 and
and 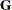 sorted differently:
sorted differently:
random int a / subject=block;
![\begin{align*} \bZ & = \left[ \begin{array}{cccccccccccccccc} 1 & 1 & & & & & & & & & & & & & & \\ 1 & 1 & & & & & & & & & & & & & & \\ 1 & & 1 & & & & & & & & & & & & & \\ 1 & & 1 & & & & & & & & & & & & & \\ 1 & & & 1 & & & & & & & & & & & & \\ 1 & & & 1 & & & & & & & & & & & & \\ & & & & 1 & 1 & & & & & & & & & & \\ & & & & 1 & 1 & & & & & & & & & & \\ & & & & 1 & & 1 & & & & & & & & & \\ & & & & 1 & & 1 & & & & & & & & & \\ & & & & 1 & & & 1 & & & & & & & & \\ & & & & 1 & & & 1 & & & & & & & & \\ & & & & & & & & 1 & 1 & & & & & & \\ & & & & & & & & 1 & 1 & & & & & & \\ & & & & & & & & 1 & & 1 & & & & & \\ & & & & & & & & 1 & & 1 & & & & & \\ & & & & & & & & 1 & & & 1 & & & & \\ & & & & & & & & 1 & & & 1 & & & & \\ & & & & & & & & & & & & 1 & 1 & & \\ & & & & & & & & & & & & 1 & 1 & & \\ & & & & & & & & & & & & 1 & & 1 & \\ & & & & & & & & & & & & 1 & & 1 & \\ & & & & & & & & & & & & 1 & & & 1 \\ & & & & & & & & & & & & 1 & & & 1 \\ \end{array} \right] \\ \bG & = \left[ \begin{array}{ccccccccccccccc} \sigma ^2_ B & & & & & & & & \\ & \sigma ^2_{AB} & & & & & & & \\ & & \sigma ^2_{AB} & & & & & & \\ & & & \sigma ^2_{AB} & & & & & \\ & & & & \ddots & & & & & \\ & & & & & \sigma ^2_ B & & & \\ & & & & & & \sigma ^2_{AB} & & \\ & & & & & & & \sigma ^2_{AB} & \\ & & & & & & & & \sigma ^2_{AB} \\ \end{array} \right] \end{align*}](images/stathpug_hplmixed0184.png)
