The HPLMIXED Procedure
Matrix Notation
Suppose that you observe n data points 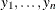 and that you want to explain them by using n values for each of p explanatory variables
and that you want to explain them by using n values for each of p explanatory variables 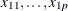 ,
, 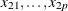 ,
, 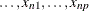 . The
. The 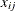 values can be either regression-type continuous variables or dummy variables that indicate class membership. The standard
linear model for this setup is
values can be either regression-type continuous variables or dummy variables that indicate class membership. The standard
linear model for this setup is
![\[ y_ i = \sum _{j=1}^ p x_{ij} \beta _ j + \epsilon _ i \quad i=1,\ldots ,n \]](images/stathpug_hplmixed0152.png)
where 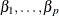 are unknown fixed-effects parameters to be estimated and
are unknown fixed-effects parameters to be estimated and 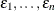 are unknown independent and identically distributed normal (Gaussian) random variables with mean 0 and variance
are unknown independent and identically distributed normal (Gaussian) random variables with mean 0 and variance 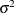 .
.
The preceding equations can be written simultaneously by using vectors and a matrix, as follows:
![\[ \left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_ n \end{array} \right] = \left[\begin{array}{cccc} x_{11} & x_{12} & \ldots & x_{1p} \\ x_{21} & x_{22} & \ldots & x_{2p} \\ \vdots & \vdots & & \vdots \\ x_{n1} & x_{n2} & \ldots & x_{np} \end{array} \right] \left[\begin{array}{c} \beta _1 \\ \beta _2 \\ \vdots \\ \beta _ p \end{array} \right] + \left[\begin{array}{c} \epsilon _1 \\ \epsilon _2 \\ \vdots \\ \epsilon _ n \end{array} \right] \]](images/stathpug_hplmixed0155.png)
For convenience, simplicity, and extendability, this entire system is written as
![\[ \mb{y} = \mb{X}\bbeta + \bepsilon \]](images/stathpug_hplmixed0001.png)
where 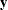 denotes the vector of observed
denotes the vector of observed 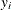 ’s,
’s, 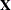 is the known matrix of
is the known matrix of 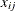 ’s,
’s, 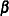 is the unknown fixed-effects parameter vector, and
is the unknown fixed-effects parameter vector, and  is the unobserved vector of independent and identically distributed Gaussian random errors.
is the unobserved vector of independent and identically distributed Gaussian random errors.
In addition to denoting data, random variables, and explanatory variables in the preceding fashion, the subsequent development
makes use of basic matrix operators such as transpose ( ), inverse (
), inverse (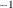 ), generalized inverse (
), generalized inverse ( ), determinant (
), determinant ( ), and matrix multiplication. See Searle (1982) for details about these and other matrix techniques.
), and matrix multiplication. See Searle (1982) for details about these and other matrix techniques.
