The HPNLMOD Procedure
Models that are estimated by PROC HPNLMOD can be represented by using the equations
![\begin{align*} \mb {Y} & = \mb {f}(\bbeta ;\mb {z}_1,\cdots ,\mb {z}_ k) + \bepsilon \\ \mr {E}[\bepsilon ] & = \mb {0} \\ \mr {Var}[\bepsilon ] & = \sigma ^2\mb {I} \end{align*}](images/stathpug_hpnlin0065.png)
where
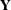
-
is the
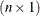 vector of observed responses
vector of observed responses
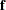
-
is the nonlinear prediction function of parameters and regressor variables
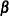
-
is the vector of model parameters to be estimated
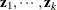
-
are the
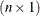 vectors for each of the
vectors for each of the 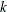 regressor variables
regressor variables

-
is the
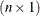 vector of residuals
vector of residuals
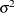
-
is the variance of the residuals
In these models, the distribution of the residuals is not specified and the model parameters are estimated using the least squares method. For the standard errors and confidence limits in the “ParameterEstimates” table to apply, the errors are assumed to be homoscedastic, uncorrelated, and have zero mean.
