The HPLOGISTIC Procedure

Existence of Maximum Likelihood Estimates

The likelihood equation for a logistic regression model does not always have a finite solution. Sometimes there is a nonunique maximum on the boundary of the parameter space, at infinity. The existence, finiteness, and uniqueness of maximum likelihood estimates for the logistic regression model depend on the patterns of data points in the observation space (Albert and Anderson, 1984; Santner and Duffy, 1986).

Consider a binary response model. Let $Y_ j$ be the response of the jth subject, and let $\mb {x}_ j$ be the vector of explanatory variables (including the constant 1 that is associated with the intercept). There are three mutually exclusive and exhaustive types of data configurations: complete separation, quasi-complete separation, and overlap.

Complete Separation

There is a complete separation of data points if there exists a vector 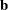$\mb {b}$ that correctly allocates all observations to their response groups; that is,

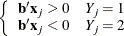
$\begin{eqnarray*} \left\{ \begin{array}{ll} \mb {b}’\mb {x}_ j > 0 & Y_ j = 1 \\ \mb {b}’\mb {x}_ j < 0 & Y_ j = 2 \end{array} \right. \end{eqnarray*}$

This configuration produces nonunique infinite estimates. If the iterative process of maximizing the likelihood function is allowed to continue, the log likelihood diminishes to 0, and the dispersion matrix becomes unbounded.

Quasi-complete Separation

The data are not completely separable, but there is a vector 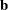$\mb {b}$ such that

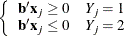
$\begin{eqnarray*} \left\{ \begin{array}{ll} \mb {b}’\mb {x}_ j \geq 0 & Y_ j = 1 \\ \mb {b}’\mb {x}_ j \leq 0 & Y_ j = 2 \end{array} \right. \end{eqnarray*}$

and equality holds for at least one subject in each response group. This configuration also yields nonunique infinite estimates. If the iterative process of maximizing the likelihood function is allowed to continue, the dispersion matrix becomes unbounded and the log likelihood diminishes to a nonzero constant.

Overlap

If neither complete nor quasi-complete separation exists in the sample points, there is an overlap of sample points. In this configuration, the maximum likelihood estimates exist and are unique.

The HPLOGISTIC procedure uses a simple empirical approach to recognize the data configurations that lead to infinite parameter estimates. The basis of this approach is that any convergence method of maximizing the log likelihood must yield a solution that indicates complete separation, if such a solution exists. Upon convergence, if the predicted response equals the observed response for every observation, there is a complete separation of data points.

If the data are not completely separated, if an observation is identified to have an extremely large probability ( $\ge$ 0.95) of predicting the observed response, and if there have been at least eight iterations, then there are two possible situations. First, there is overlap in the data set, the observation is an atypical observation of its own group, and the iterative process stopped when a maximum was reached. Second, there is quasi-complete separation in the data set, and the asymptotic dispersion matrix is unbounded. If any of the diagonal elements of the dispersion matrix for the standardized observation vector (all explanatory variables standardized to zero mean and unit variance) exceeds 5,000, quasi-complete separation is declared. If either complete separation or quasi-complete separation is detected, a note is displayed in the procedure output.

Checking for quasi-complete separation is less foolproof than checking for complete separation. If neither type of separation is discovered and your parameter estimates have large standard errors, then this indicates that your data might be separable. The NOCHECK option in the MODEL statement turns off the process of checking for infinite parameter estimates.