The HPLOGISTIC Procedure

Log-Likelihood Functions

Subsections:

Binary Distribution
Binomial Distribution
Multinomial Distribution

The HPLOGISTIC procedure forms the log-likelihood functions of the various models as

$L(\bmu ;\mb {y}) = \sum _{i=1}^{n} f_ i \, l(\mu _ i;y_ i,w_ i)$

where $l(\mu _ i;y_ i,w_ i)$ is the log-likelihood contribution of the $i$ th observation with weight $w_ i$ and $f_ i$ is the value of the frequency variable. For the determination of $w_ i$ and $f_ i$ , see the WEIGHT and FREQ statements. The individual log-likelihood contributions for the various distributions are as follows.

Binary Distribution

The HPLOGISTIC procedure computes the log-likelihood function $l(\mu _ i(\bbeta );y_ i)$ for the $i$ th binary observation as

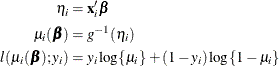
$\begin{align*} \eta _ i & = \mb {x}_ i’\bbeta \\ \mu _ i(\bbeta ) & = g^{-1}(\eta _ i) \\ l(\mu _ i(\bbeta );y_ i) & = y_ i \log \{ \mu _ i\} + (1-y_ i)\log \{ 1-\mu _ i\} \end{align*}$

Here, $\mu _ i$ is the probability of an event, and the variable $y_ i$ takes on the value 1 for an event and the value 0 for a non-event. The inverse link function $g^{-1}(\cdot )$ maps from the scale of the linear predictor $\eta _ i$ to the scale of the mean. For example, for the logit link (the default),

$\mu _ i(\bbeta ) = \frac{\exp \{ \eta _ i\} }{1+\exp \{ \eta _ i\} }$

You can control which binary outcome in your data is modeled as the event with the response-options in the MODEL statement, and you can choose the link function with the LINK= option in the MODEL statement.

If a WEIGHT statement is given and $w_ i$ denotes the weight for the current observation, the log-likelihood function is computed as

$l(\mu _ i(\bbeta );y_ i,w_ i) = w_ i l(\mu _ i(\bbeta );y_ i)$

Binomial Distribution

The HPLOGISTIC procedure computes the log-likelihood function $l(\mu _ i(\bbeta );y_ i)$ for the $i$ th binomial observation as

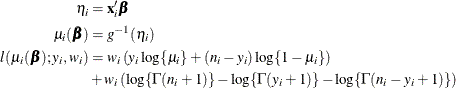
$\begin{align*} \eta _ i & = \mb {x}_ i’\bbeta \\ \mu _ i(\bbeta ) & = g^{-1}(\eta _ i) \\ l(\mu _ i(\bbeta );y_ i,w_ i) & = w_ i \left( y_ i \log \{ \mu _ i\} + (n_ i - y_ i) \log \{ 1-\mu _ i\} \right) \\ & + w_ i \left( \log \{ \Gamma (n_ i+1)\} - \log \{ \Gamma (y_ i+1)\} - \log \{ \Gamma (n_ i-y_ i+1)\} \right) \end{align*}$

where $y_ i$ and $n_ i$ are the values of the events and trials of the $i$ th observation, respectively. $\mu _ i$ measures the probability of events (successes) in the underlying Bernoulli distribution whose aggregate follows the binomial distribution.

Multinomial Distribution

The multinomial distribution modeled by the HPLOGISTIC procedure is a generalization of the binary distribution; it is the distribution of a single draw from a discrete distribution with $J$ possible values. The log-likelihood function for the $i$ th observation is thus deceptively simple:

$l(\bmu _ i;\mb {y}_ i,w_ i) = w_ i \sum _{j=1}^{J} y_{ij}\log \{ \mu _{ij}\}$

In this expression, $J$ denotes the number of response categories (the number of possible outcomes) and $\mu _{ij}$ is the probability that the $i$ th observation takes on the response value associated with category $j$ . The category probabilities must satisfy

$\sum _{j=1}^{J} \mu _ j = 1$

and the constraint is satisfied by modeling $J-1$ categories. In models with ordered response categories, the probabilities are expressed in cumulative form, so that the last category is redundant. In generalized logit models (multinomial models with unordered categories), one category is chosen as the reference category and the linear predictor in the reference category is set to zero.