OUTPUT Statement :: SAS/STAT(R) 13.1 User's Guide: High-Performance Procedures

OUTPUT Statement

OUTPUT <OUT=SAS-data-set>
<keyword <=name>>…<keyword <=name>> </ options> ;

The OUTPUT statement creates a data set that contains observationwise statistics that are computed after the model is fitted. The variables in the input data set are not included in the output data set to avoid data duplication for large data sets; however, variables that are specified in the ID statement are included.

If the input data are in distributed form, where accessing data in a particular order cannot be guaranteed, the HPGENSELECT procedure copies the distribution or partition key to the output data set so that its contents can be joined with the input data.

The computation of the output statistics is based on the final parameter estimates. If the model fit does not converge, missing values are produced for the quantities that depend on the estimates.

When there are more than two response levels for multinomial data, values are computed only for variables that are named by the XBETA and PREDICTED keywords; the other variables have missing values. These statistics are computed for every response category, and the automatic variable _LEVEL_ identifies the response category on which the computed values are based. If you also specify the OBSCAT option, then the observationwise statistics are computed only for the observed response category, as indicated by the value of the _LEVEL_ variable.

For observations in which only the response variable is missing, values of the XBETA and PREDICTED statistics are computed even though these observations do not affect the model fit. For zero-inflated models, ZBETA and PZERO are also computed. This practice enables predicted mean values or predicted probabilities to be computed for new observations.

You can specify the following syntax elements in the OUTPUT statement before the slash (/).

OUT=SAS-data-set DATA=SAS-data-set

specifies the name of the output data set. If the OUT= (or DATA=) option is omitted, the procedure uses the DATAn convention to name the output data set.

keyword <=name>

specifies a statistic to include in the output data set and optionally assigns a name to the variable. If you do not provide a name, the HPGENSELECT procedure assigns a default name based on the type of statistic requested.

You can specify the following keywords for adding statistics to the OUTPUT data set:

ADJPEARSON | ADJPEARS | STDRESCHI

requests the Pearson residual, adjusted to have unit variance. The adjusted Pearson residual is defined for the ith observation as 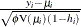$\frac{y_ i-\mu _ i}{\sqrt {\phi \mr {V}(\mu _ i)(1-h_ i)}}$ , where 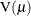$\mr {V}(\mu )$ is the response distribution variance function and 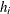$h_ i$ is the leverage. The leverage 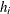$h_ i$ of the ith observation is defined as the ith diagonal element of the hat matrix

$\bH = \bW ^\frac {1}{2}\bX (\bX ^{\prime }\bW \bX )^{-1}\bX ^{\prime }\bW ^\frac {1}{2}$

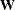where $\bW$ is the diagonal matrix that has 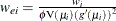$w_{ei}=\frac{w_ i}{\phi \mr {V}(\mu _ i)(g^{\prime }(\mu _ i))^2}$ as the ith diagonal, and 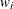$w_ i$ is a prior weight specified by a WEIGHT statement or 1 if no WEIGHT statement is specified. For the negative binomial, 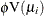$\phi \mr {V}(\mu _ i)$ in the denominator is replaced with the distribution variance, in both the definition of the leverage and the adjusted residual.

This statistic is not computed for multinomial models, nor is it computed for zero-modified models.

LINP | XBETA

requests the linear predictor 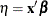$\eta =\mb {x}’\bbeta$ .

LOWER

requests a lower confidence limit for the predicted value. This statistic is not computed for generalized logit multinomial models or zero-modified models.

PEARSON | PEARS | RESCHI

requests the Pearson residual, 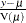$\frac{y-\mu }{\mr {V}(\mu )}$ , where 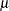$\mu$ is the estimate of the predicted response mean and 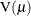$\mr {V}(\mu )$ is the response distribution variance function. 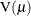For the negative binomial defined in the section Negative Binomial Distribution and the zero-inflated models defined in the sections Zero-Inflated Poisson Distribution and Zero-Inflated Negative Binomial Distribution, the distribution variance is used in place of $\mr {V}(\mu )$ .

This statistic is not computed for multinomial models.

PREDICTED | PRED | P

requests predicted values for the response variable.

PZERO

requests zero-inflation probabilities for zero-inflated models.

RESIDUAL | RESID | R

requests the raw residual, 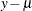$y-\mu$ , where 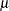$\mu$ is the estimate of the predicted mean. This statistic is not computed for multinomial models.

UPPER

requests an upper confidence limit for the predicted value. This statistic is not computed for generalized logit multinomial models or zero-modified models.

ZBETA

requests the linear predictor for the zeros model in zero-modified models: 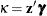$\kappa = \mb {z}’\bgamma$ .

You can specify the following options in the OUTPUT statement after the slash (/):

ALPHA=number: specifies the significance level for the construction of confidence intervals in the OUTPUT data set. The confidence level is $1-\Argument{number}$ .
OBSCAT: requests (for multinomial models) that observationwise statistics be produced only for the response level. If the OBSCAT option is not specified and the response variable has $J$ levels, then the following outputs are created: for cumulative link models, $J-1$ records are output for every observation in the input data that corresponds to the $J-1$ lower-ordered response categories; for generalized logit models, $J$ records are output that correspond to all $J$ response categories.

The HPGENSELECT Procedure

OUTPUT Statement