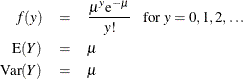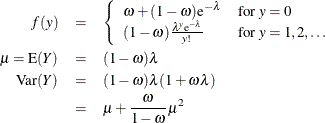The HPGENSELECT Procedure
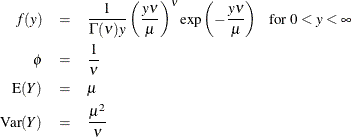
For the gamma distribution, ![]() is the estimated dispersion parameter that is displayed in the output. The parameter
is the estimated dispersion parameter that is displayed in the output. The parameter ![]() is also sometimes called the gamma index parameter.
is also sometimes called the gamma index parameter.
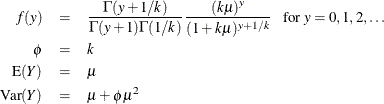
For the negative binomial distribution, k is the estimated dispersion parameter that is displayed in the output.
The Tweedie model is a generalized linear model from the exponential family. The Tweedie distribution is characterized by
three parameters: the mean parameter ![]() , the dispersion
, the dispersion ![]() , and the power p. The variance of the distribution is
, and the power p. The variance of the distribution is ![]() . For values of p in the range
. For values of p in the range ![]() , a Tweedie random variable can be represented as a Poisson sum of gamma distributed random variables. That is,
, a Tweedie random variable can be represented as a Poisson sum of gamma distributed random variables. That is,
where N has a Poisson distribution that has mean ![]() and the
and the ![]() have independent, identical gamma distributions, each of which has an expected value
have independent, identical gamma distributions, each of which has an expected value ![]() and an index parameter
and an index parameter ![]() .
.
In this case, Y has a discrete mass at 0, ![]() , and the probability density of Y
, and the probability density of Y ![]() is represented by an infinite series for
is represented by an infinite series for ![]() . The HPGENSELECT procedure restricts the power parameter to satisfy
. The HPGENSELECT procedure restricts the power parameter to satisfy ![]() for numerical stability in model fitting. The Tweedie distribution does not have a general closed form representation for
all values of p. It can be characterized in terms of the distribution mean parameter
for numerical stability in model fitting. The Tweedie distribution does not have a general closed form representation for
all values of p. It can be characterized in terms of the distribution mean parameter ![]() , dispersion parameter
, dispersion parameter ![]() , and power parameter p. For more information about the Tweedie distribution, see Frees (2010).
, and power parameter p. For more information about the Tweedie distribution, see Frees (2010).
The distribution mean and variance are given by:
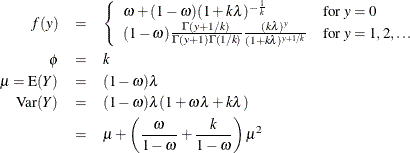
For the zero-inflated negative binomial distribution, k is the estimated dispersion parameter that is displayed in the output.

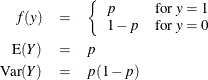
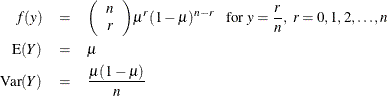
![\begin{eqnarray*} f(y) & = & \frac{1}{\sqrt {2\pi y^3} \sigma } \exp \left[ -\frac{1}{2y} \left( \frac{y-\mu }{\mu \sigma } \right)^2 \right]~ ~ ~ \mbox{for } 0 < y < \infty \\ \phi & = & \sigma ^2 \\ \mr {Var}(Y) & = & \phi \mu ^3 \\ \end{eqnarray*}](images/stathpug_hpgenselect0074.png)
![\begin{eqnarray*} f(y) & = & \frac{1}{\sqrt {2\pi } \sigma } \exp \left[ -\frac{1}{2} \left( \frac{y-\mu }{\sigma } \right)^2 \right]~ ~ ~ \mbox{for } -\infty < y < \infty \\ \phi & = & \sigma ^{2} \\ \mr {E}(Y) & = & \mu \\ \mr {Var}(Y) & = & \phi \\ \end{eqnarray*}](images/stathpug_hpgenselect0077.png)