HISTOGRAM Statement: CAPABILITY Procedure
Note: See Comparing Goodness-of-Fit Tests in the SAS/QC Sample Library.
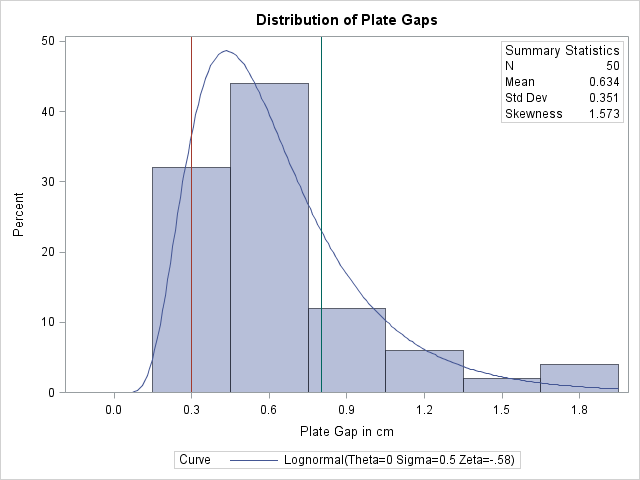
A weakness of the chi-square goodness-of-fit test is its dependence on the choice of histogram midpoints. An advantage of the EDF tests is that they give the same results regardless of the midpoints, as illustrated in this example.
In Example 5.9, the option MIDPOINTS=0.2 TO 1.8 BY 0.2 was used to specify the histogram midpoints for Gap. The following statements refit the lognormal distribution by using default midpoints (0.3 to 1.8 by 0.3).
data Plates; label Gap='Plate Gap in cm'; input Gap @@; datalines; 0.746 0.357 0.376 0.327 0.485 1.741 0.241 0.777 0.768 0.409 0.252 0.512 0.534 1.656 0.742 0.378 0.714 1.121 0.597 0.231 0.541 0.805 0.682 0.418 0.506 0.501 0.247 0.922 0.880 0.344 0.519 1.302 0.275 0.601 0.388 0.450 0.845 0.319 0.486 0.529 1.547 0.690 0.676 0.314 0.736 0.643 0.483 0.352 0.636 1.080 ;
title1 'Distribution of Plate Gaps';
proc capability data=Plates noprint;
var Gap;
specs lsl = 0.3 usl = 0.8;
histogram / lognormal
nospeclegend
odstitle = title;
inset n mean(5.3) std='Std Dev'(5.3) skewness(5.3) /
pos = ne
header = 'Summary Statistics';
run;
The histogram is shown in Output 5.10.1.
A summary of the lognormal fit is shown in Output 5.10.2. The p-value for the chi-square goodness-of-fit test is 0.082. Because this value is less than 0.10 (a typical cutoff level), the conclusion is that the lognormal distribution is not an appropriate model for the data. This is the opposite conclusion drawn from the chi-square test in Example 5.9, which is based on a different set of midpoints and has a p-value of 0.2756 (see Output 5.9.2). Moreover, the results of the EDF goodness-of-fit tests are the same because these tests do not depend on the midpoints. When available, the EDF tests provide more powerful alternatives to the chi-square test. For a thorough discussion of EDF tests, refer to D’Agostino and Stephens (1986).