QQPLOT Statement: CAPABILITY Procedure
Creating a Normal Quantile-Quantile Plot
See CAPQQ1 in the SAS/QC Sample LibraryMeasurements of the distance between two holes cut into 50 steel sheets are saved as values of the variable Distance in the following data set:
data Sheets; input Distance @@; label Distance='Hole Distance in cm'; datalines; 9.80 10.20 10.27 9.70 9.76 10.11 10.24 10.20 10.24 9.63 9.99 9.78 10.10 10.21 10.00 9.96 9.79 10.08 9.79 10.06 10.10 9.95 9.84 10.11 9.93 10.56 10.47 9.42 10.44 10.16 10.11 10.36 9.94 9.77 9.36 9.89 9.62 10.05 9.72 9.82 9.99 10.16 10.58 10.70 9.54 10.31 10.07 10.33 9.98 10.15 ;
The cutting process is in control, and you decide to check whether the process distribution is normal. The following statements
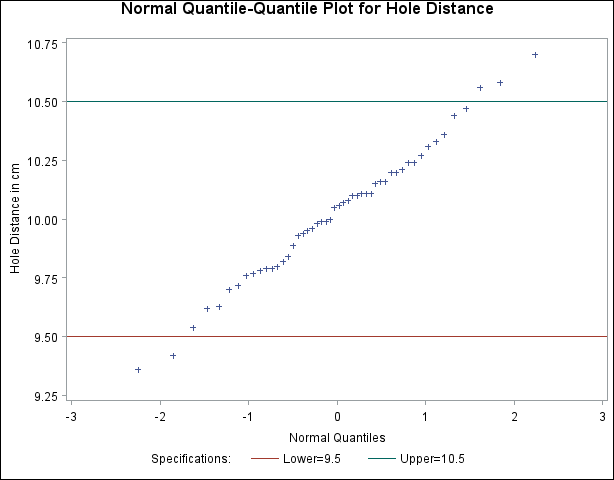
create a Q-Q plot for Distance, shown in Figure 5.39, with lower and upper specification lines at 9.5 cm and 10.5 cm:[24]
ods graphics off; symbol v=plus; title 'Normal Quantile-Quantile Plot for Hole Distance'; proc capability data=Sheets noprint; spec lsl=9.5 usl=10.5; qqplot Distance; run;
The plot compares the ordered values of Distance with quantiles of the normal distribution. The linearity of the point pattern indicates that the measurements are normally
distributed. Note that a normal Q-Q plot is created by default. The specification lines are requested with the LSL= and USL= options in the SPEC statement.
Figure 5.39: Normal Quantile-Quantile Plot Created with Traditional Graphics
[24] For a P-P plot using these data, see Figure 5.31. For a probability plot using these data, see Example 5.20.
