QQPLOT Statement: CAPABILITY Procedure
Interpretation of Quantile-Quantile and Probability Plots
The following properties of Q-Q plots and probability plots make them useful diagnostics of how well a specified theoretical distribution fits a set of measurements:
-
If the quantiles of the theoretical and data distributions agree, the plotted points fall on or near the line
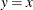 .
.
-
If the theoretical and data distributions differ only in their location or scale, the points on the plot fall on or near the line
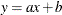 . The slope a and intercept b are visual estimates of the scale and location parameters of the theoretical distribution.
. The slope a and intercept b are visual estimates of the scale and location parameters of the theoretical distribution.
Q-Q plots are more convenient than probability plots for graphical estimation of the location and scale parameters since the x-axis of a Q-Q plot is scaled linearly. On the other hand, probability plots are more convenient for estimating percentiles or probabilities.
There are many reasons why the point pattern in a Q-Q plot may not be linear. Chambers et al. (1983) and Fowlkes (1987) discuss the interpretations of commonly encountered departures from linearity, and these are summarized in the following table.
Table 5.70: Quantile-Quantile Plot Diagnostics
|
Description of Point Pattern |
Possible Interpretation |
|---|---|
|
All but a few points fall on a line |
Outliers in the data |
|
Left end of pattern is below the line; right end of pattern is above the line |
Long tails at both ends of the data distribution |
|
Left end of pattern is above the line; right end of pattern is below the line |
Short tails at both ends of the data distribution |
|
Curved pattern with slope increasing from left to right |
Data distribution is skewed to the right |
|
Curved pattern with slope decreasing from left to right |
Data distribution is skewed to the left |
|
Staircase pattern (plateaus and gaps) |
Data have been rounded or are discrete |
In some applications, a nonlinear pattern may be more revealing than a linear pattern. However, Chambers et al. (1983) note that departures from linearity can also be due to chance variation.
