PROC RELIABILITY: MODEL Statement

MODEL Statement

MODEL variable<*censor-variable(values)> <=effect-list> </ options> ;

MODEL (variable1 variable2) <=effect-list> </ options> ;

You use the MODEL statement to fit regression models, where life is modeled as a function of explanatory variables.

You can use only one MODEL statement after a PROC RELIABILITY statement. If you specify more than one MODEL statement, only the last is used.

The MODEL statement does not produce any plots, but it enables you to analyze more complicated regression models than the ANALYZE, PROBPLOT, or RELATIONPLOT statement does. The probability distribution specified in the DISTRIBUTION statement is used in the analysis. The following are examples of MODEL statements:

   model time = temp voltage;
   model life*censor(1) = voltage width;

See the section Analysis of Accelerated Life Test Data and the section Regression Modeling for examples that use the MODEL statement to fit regression models.

If your data are right censored lifetime data, you must specify a censor-variable and, in parentheses, the values of the censor-variable that correspond to censored data values.

If your data are recurrent events data with exact event times, you must specify a censor-variable and, in parentheses, the values of the censor-variable that correspond to the end-of-service times for each unit under observation. In this case, you must also specify a UNITID statement to identify the specific unit that corresponds to each observation.

If your lifetime data contain any interval-censored or left-censored values, you must specify variable1 and variable2 in parentheses to provide the endpoints of the interval for each observation.

If your data are recurrent events data, and event times are not known exactly, but are known only to have occurred in intervals, you must specify variable1 and variable2 in parentheses to provide the endpoints of the interval for each observation. In this case, you must also specify a variable that determines the number of events observed in each interval with a FREQ statement, and a variable that determines the number of units under observation in each interval with a NENTER statement.

The independent variables in your regression model are specified in the effect-list. The effect-list is any combination of continuous variables, classification variables, and interaction effects.

See the section Regression Models for further information on specifying the independent variables.

The elements of the MODEL statement are described as follows.

variable

is the dependent, or response, variable. The variable must be a numeric variable in the input data set.

censor-variable(values)

for lifetime data, indicates which observations in the input data set are right censored. You specify the values of censor-variable that represent censored observations by placing those values in parentheses after the variable name. If your data are not right censored, then you can omit the specification of a censor-variable; otherwise, censor-variable must be a numeric variable in the input data set.

If your data are recurrent events data and exact event times are known, then you must specify censor-variable. If censor-variable is equal to one of the values, then the value of variable is the end of observation time for a unit. Otherwise, you use censor-variable to assign a cost to the event that occurs at the value of variable. If all events have unit cost, then censor-variable should be set to one for all observations that do not correspond to end of observation times. The censor-variable plays the same role as the cost/censor-variable in the MCFPLOT statement in this case.

(variable1 variable2)

is another method of specifying the dependent variable in a regession model for lifetime data. You can use this syntax in a situation where uncensored, interval-censored, left-censored, and right-censored values occur in the same set of data. Table 14.27 shows how you use this syntax to specify different types of censoring by using combinations of missing and nonmissing values.

Table 14.27 Specifying Censored Values
Variable1	Variable2	Type of Censoring
Nonmissing	Nonmissing	Uncensored if variable1 = variable2
Nonmissing	Nonmissing	Interval censored if variable1 < variable2
Nonmissing	Missing	Right censored at variable1
Missing	Nonmissing	Left censored at variable2

For example, if T1 and T2 represent time in hours in the input data set

OBS    T1    T2

 1      .     6
 2      6    12
 3     12    24
 4     24     .
 5     24    24

then the statement

   model (t1 t2);

specifies a model in which observation 1 is left censored at 6 hours, observation 2 is interval censored in the interval (6, 12), observation 3 is interval censored in (12,24), observation 4 is right censored at 24 hours, and observation 5 is an uncensored lifetime of 24 hours.

You can also use this method to specify a model for recurrent events data when exact recurrence times are not known. In this case, events are observed to have occurred in intervals specified by (variable1 variable2). The values of the variable specified in a FREQ statement determine the number of events that occurred in each interval, and the values of the variable specified in a NENTER statement determine the number of units under observation in each interval.

effect-list

is a list of variables in the input data set representing the values of the independent variables in the model for each observation, and combinations of variables representing interaction terms. If a variable in the effect-list is also listed in a CLASS statement, an indicator variable is generated for each level of the variable. An indicator variable for a particular level is equal to 1 for observations with that level, and equal to 0 for all other observations. This type of variable is called a classification variable. Classification variables can be either character or numeric. If a variable is not listed in a CLASS statement, it is assumed to be a continuous variable, and it must be numeric.

options

control how the model is fit and what output is produced. All options are specified after a slash (/) in the MODEL statement. The "Summary of Options" section, which follows, lists all options by function.

Summary of Options

Table 14.28 Model Statement Options

Option

Option Description

CONFIDENCE=number

Specifies the confidence coefficient for all confidence intervals. Specify a number between 0 and 1. The default value is 0.95.

CONVERGE=number

Specifies the convergence criterion for maximum likelihood fit. See the section Maximum Likelihood Estimation for details.

CONVH=number

Specifies the convergence criterion for the relative Hessian convergence criterion. See the section Maximum Likelihood Estimation for details.

CORRB

Requests parameter correlation matrix.

COVB

Requests parameter covariance matrix.

HPPTEST

Applies only to models for recurrent events data. This option requests a likelihood ratio test for a homogeneous Poisson process.

INEST | IN=SAS-data-set

Applies only to models for recurrent events data. This option specifies a SAS data set that can contain initial values, equality constraints, upper bounds, or lower bounds for the intercept and shape parameters in a model for recurrents events data. See the section INEST Data Set for Recurrent Events Models for details.

INITIAL=number list

Specifies initial values for regression parameters other than the location (intercept) term.

ITPRINT

Requests the iteration history for maximum likelihood fit.

LRCL

Requests likelihood ratio confidence intervals for distribution parameters.

LOCATION=number <LINIT>

Specifies the fixed or initial value of the location, or intercept parameter.

MAXIT=number

Specifies the maximum number of iterations allowed for maximum likelihood fit.

OBSTATS

Requests a table that contains the XBETA, SURV, SRESID, and ADJRESID statistics in Table 14.29. The table also contains the dependent and independent variables in the model.

OBSTATS(statistics)

Requests a table that contains the model variables and the statistics in the specified list of statistics. Available statistics are shown in Table 14.29.

ORDER=DATA | FORMATTED |

FREQ | INTERNAL

Specifies the sort order for values of the classification variables in the effect-list.

PSTABLE=number

Specifies stable parameterization. The number must be between zero and one. See the section Stable Parameters for further information.

READOUT

Analyzes data in readout structure. The FREQ statement must be used to specify the number of units that fail in each interval, and the NENTER statement must be used to specify the number of unfailed units that enter each interval.

RELATION=transformation-keyword

RELATION=(transformation-keyword1<,>transformation-keyword2)

Specifies the type of relationship between independent and dependent variables. In the first form, the transformation specified is applied to the first continuous independent variable in the model. In the second form, the transformations specified within parentheses are applied to the first two continuous independent variables in the model, in the order listed. transformation-keyword, transformation-keyword1, and transformation-keyword2 can be any of the transformations listed in the following table. See Table 14.61 for definitions of the transformations.

Transformation Keyword	Type of Transformation
ARRHENIUS	Arrhenius (Nelson parameterization)
ARRHENIUS2	Arrhenius (activation energy)
POWER	Logarithmic
LINEAR	Linear
LOGISTIC	Logistic

SCALE=number <SCINIT>

Specifies a fixed or initial value of scale parameter.

SHAPE=number <SHINIT>

Specifies a fixed or initial value of shape parameter.

SINGULAR=number

Specifies the singularity criterion for matrix inversion.

THRESHOLD=number

Specifies a fixed threshold parameter. See Table 14.51 for the distributions with a threshold parameter.

WALDCL|NORMALCL

Requests Wald type confidence intervals for distribution parameters. See Table 14.62 and Table 14.68 for details about the computation of Wald confidence intervals. This is the default option used if likelihood ratio confidence intervals are not requested by using the LRCL option.

Table 14.29 Available Statistics Computed for Each Observation with the OBSTATS Option

Option

Option Description

CENSOR

Is a variable that indicates the type of censoring for each opservation in the input data set. The possible values for CENSOR and their interpretations are listed in the following table.

Type of Response	CENSOR Variable Value
Uncensored	0
Right-censored	1
Left-censored	2
Interval-censored	3

CONTROL=variable

Specifies a control variable in the input data set that allows the computation of statistics for a subset of observations in the input data set. If the value of variable is 1, the statistics are computed for that observation. If the value of the control variable is not equal to 1, the statistics are not computed for that observation.

QUANTILES | QUANTILE |

Q=number-list

Requests distribution quantiles for each number in number-list for each observation. The numbers must be between 0 and 1. Estimated quantile standard errors, and upper and lower confidence limits are also tabulated.

XBETA

Specifies the linear predictor.

SURVIVAL | SURV

Specifies the fitted survival function, evaluated at the value of the dependent variable.

RESID

Specifies the raw residual.

SRESID

Specifies the standardized residual.

GRESID

Specifies the modified Cox-Snell residual.

DRESID

Specifies the deviance residual.

ADJRESID

Specifies the adjusted standardized residuals. These are adjusted for right-censored observations by adding the median of the lifetime greater than the right-censored values to the residuals.

RESIDADJ=number

Specifies the adjustment to be added to Cox-Snell residual for right-censored data values. The default is log(2) = 0.693.

RESIDALPHA | RALPHA=number

Specifies that the number 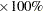$\text{[math]}$ percentile residual lifetime used to adjust right-censored standardized residuals. The number must be between 0 and 1. The default value is 0.5, which corresponds to the median.