PPPLOT Statement: CAPABILITY Procedure
Summary of Theoretical Distributions
You can use the PPPLOT statement to request P-P plots based on the theoretical distributions summarized in the following table:
Parameters |
||||||
|---|---|---|---|---|---|---|
Family |
Distribution Function |
Range |
Location |
Scale |
Shape |
|
Beta |
|
|
|
|
|
|
Exponential |
|
|
|
|
||
Gamma |
|
|
|
|
|
|
Gumbel |
|
all |
|
|
||
Inverse Gaussian |
|
|
|
|
||
|
||||||
Lognormal |
|
|
|
|
|
|
Normal |
|
all |
|
|
||
Generalized Pareto |
|
all |
|
|
|
|
Power Function |
|
|
|
|
|
|
Rayleigh |
|
|
|
|
||
Weibull |
|
|
|
|
|
|
You can request these distributions with the BETA, EXPONENTIAL, GAMMA, GUMBEL, IGAUSS, NORMAL, LOGNORMAL, PARETO, POWER, RAYLEIGH, and WEIBULL options, respectively. If you do not specify a distribution option, a normal P-P plot is created.
To create a P-P plot, you must provide all of the parameters for the theoretical distribution. If you do not specify parameters, then default values or estimates are substituted, as summarized by the following table:
Family |
Default Values |
Estimated Values |
|---|---|---|
Beta |
|
maximum likelihood estimates for |
Exponential |
|
maximum likelihood estimate for |
Gamma |
|
maximum likelihood estimates for |
Gumbel |
None |
maximum likelihood estimates for |
Inverse Gaussian |
None |
sample estimate for |
Lognormal |
|
maximum likelihood estimates for |
Normal |
None |
sample estimates for |
Generalized Pareto |
|
maximum likelihood estimates for |
Power Function |
|
maximum likelihood estimate for |
Rayleigh |
|
maximum likelihood estimate for |
Weibull |
|
maximum likelihood estimates for |

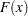
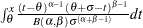
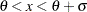


 ,
, 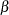
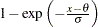
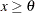
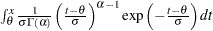
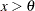
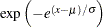

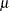
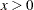
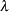
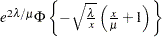
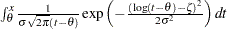
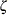
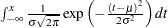
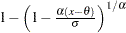
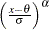

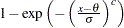

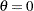 ,
,