| The UNIVARIATE Procedure |
Example 4.33 Estimating Parameters from Lognormal Quantile Plots
This example, which is a continuation of Example 4.31, demonstrates techniques for estimating the shape, location, and scale parameters, and the theoretical percentiles for a two-parameter lognormal distribution.
If the threshold parameter is known, you can construct a two-parameter lognormal Q-Q plot by subtracting the threshold from the data values and making a normal Q-Q plot of the log-transformed differences, as illustrated in the following statements:
data ModifiedMeasures; set Measures; LogDiameter = log(Diameter-5); label LogDiameter = 'log(Diameter-5)'; run;
symbol v=plus;
title 'Two-Parameter Lognormal Q-Q Plot for Diameters';
proc univariate data=ModifiedMeasures noprint;
qqplot LogDiameter / normal(mu=est sigma=est)
square
vaxis=axis1;
inset n mean (5.3) std (5.3)
/ pos = nw header = 'Summary Statistics';
axis1 label=(a=90 r=0);
run;
Output 4.33.1
Two-Parameter Lognormal Q-Q Plot for Diameters
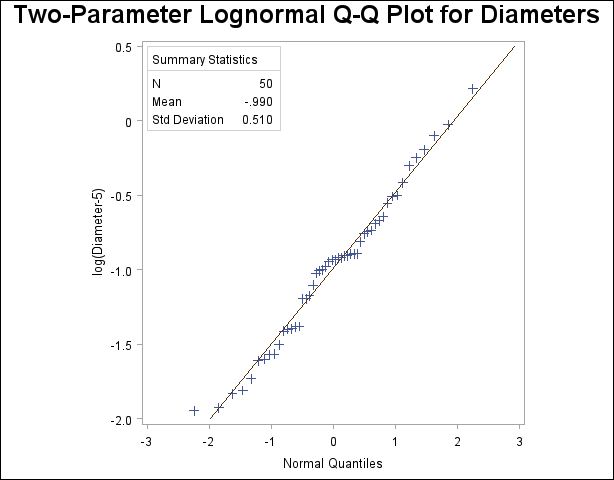
Because the point pattern in Output 4.33.1 is linear, you can estimate the lognormal parameters
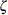 and
and  as the normal plot estimates of
as the normal plot estimates of 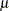 and
and  , which are
, which are  0.99 and 0.51. These values correspond to the previous estimates of
0.99 and 0.51. These values correspond to the previous estimates of  0.92 for
0.92 for 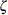 and 0.5 for
and 0.5 for  from Example 4.31. A sample program for this example, uniex18.sas, is available in the SAS Sample Library for Base SAS software.
from Example 4.31. A sample program for this example, uniex18.sas, is available in the SAS Sample Library for Base SAS software. Copyright © SAS Institute, Inc. All Rights Reserved.