The OPTNET Procedure

Overview: OPTNET Procedure

The OPTNET procedure includes a number of graph theory, combinatorial optimization, and network analysis algorithms. The algorithm classes are listed in Table 2.1.

Table 2.1: Algorithm Classes in PROC OPTNET

Algorithm Class	PROC OPTNET Statement
Biconnected components	BICONCOMP
Maximal cliques	CLIQUE
Connected components	CONCOMP
Cycle detection	CYCLE
Weighted matching	LINEAR_ASSIGNMENT
Minimum-cost network flow	MINCOSTFLOW
Minimum cut	MINCUT
Minimum spanning tree	MINSPANTREE
Shortest path	SHORTPATH
Transitive closure	TRANSITIVE_CLOSURE
Traveling salesman	TSP

You can use the OPTNET procedure to analyze relationships between entities. These relationships are typically defined by using a graph. A graph 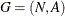$G = (N,A)$ is defined over a set N of nodes and a set A of arcs. A node is an abstract representation of some entity (or object), and an arc defines some relationship (or connection) between two nodes. The terms node and vertex are often interchanged in describing an entity. The term arc is often interchanged with the term edge or link when describing a connection.

You can also access these network algorithms via the network solver in PROC OPTMODEL. For more information, see the network solver chapter in SAS/OR User's Guide: Mathematical Programming.