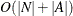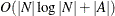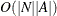The OPTNET Procedure

Shortest Path

Subsections:

Output Data Sets
Shortest Paths for All Pairs
Shortest Paths for a Subset of Source-Sink Pairs
Shortest Paths for a Subset of Source or Sink Pairs
Shortest Paths for One Source-Sink Pair
Shortest Paths with Auxiliary Weight Calculation
Shortest Paths with Negative Link Weights

A shortest path between two nodes u and v in a graph is a path that starts at u and ends at v and has the lowest total link weight. The starting node is called the source node, and the ending node is called the sink node.

In PROC OPTNET, you can calculate shortest paths by using the SHORTPATH statement. The options for this statement are described in the section SHORTPATH Statement.

The shortest path algorithm reports status information in a macro variable called _OROPTNET_SHORTPATH_. For more information about this macro variable, see the section Macro Variable _OROPTNET_SHORTPATH_.

By default, PROC OPTNET finds shortest paths for all pairs. That is, it finds a shortest path for each possible combination of source and sink nodes. Alternatively, you can use the SOURCE= option to fix a particular source node and find shortest paths from the fixed source node to all possible sink nodes. Conversely, by using the SINK= option, you can fix a sink node and find shortest paths from all possible source nodes to the fixed sink node. By using both options together, you can request one particular shortest path for a specific source-sink pair. In addition, you can use the DATA_NODES_SUB= option to define a list of source-sink pairs to process, as described in the section Node Subset Input Data. The following sections show examples of these options.

Which algorithm PROC OPTNET uses to find shortest paths depends on the data. The algorithm and run-time complexity for each link type are shown in Table 2.33.

Table 2.33: Algorithms for Shortest Paths

Link Type	Algorithm	Complexity (per Source Node)
Unweighted	Breadth-first search	$O(\|N\|+\|A\|)$
Weighted (nonnegative)	Dijkstra’s algorithm	$O(\|N\| \log \|N\| + \|A\|)$
Weighted (positive and negative allowed)	Bellman-Ford algorithm	$O(\|N\|\|A\|)$

Details for each algorithm can be found in Ahuja, Magnanti, and Orlin (1993).

For weighted graphs, the algorithm uses the weight variable that is defined in the links data set to evaluate a path’s total weight (cost). You can also use the WEIGHT2= option in the SHORTPATH statement to define an auxiliary weight. The auxiliary weight is not used in the algorithm to evaluate a path’s total weight. It is calculated only for the sake of reporting the total auxiliary weight for each shortest path.

Output Data Sets

The shortest path algorithm produces up to two output data sets. The output data set that you specify in the OUT_PATHS= option contains the links of a shortest path for each source-sink pair combination. The output data set that you specify in the OUT_WEIGHTS= option contains the total weight for the shortest path for each source-sink pair combination.

OUT_PATHS= Data Set

The OUT_PATHS= data set contains the links present in the shortest path for each source-sink pair. For large graphs and a large requested number of source-sink pairs, this output data set can be extremely large. For extremely large sets, generating the output can sometimes take longer than computing the shortest paths. For example, using the US road network data for the state of New York, the data contain a directed graph that has 264,346 nodes. Finding the shortest path for all pairs from only one source node results in 140,969,120 observations, which is a data set of size 11 GB. Finding shortest paths for all pairs from all nodes would produce an enormous output data set.

The OUT_PATHS= data set contains the following columns:

source: the source node label of this shortest path
sink: the sink node label of this shortest path
order: for this source-sink pair, the order of this link in a shortest path
from: the from node label of this link in a shortest path
to: the to node label of this link in a shortest path
weight: the weight of this link in a shortest path
weight2: the auxiliary weight of this link

OUT_WEIGHTS= Data Set

The OUT_WEIGHTS= data set contains the total weight (and total auxiliary weight) for the shortest path for each source-sink pair.

This data set contains the following columns:

source: the source node label of this shortest path
sink: the sink node label of this shortest path
path_weight: the total weight of the shortest path for this source-sink pair
path_weight2: the total auxiliary weight of the shortest path for this source-sink pair

Shortest Paths for All Pairs

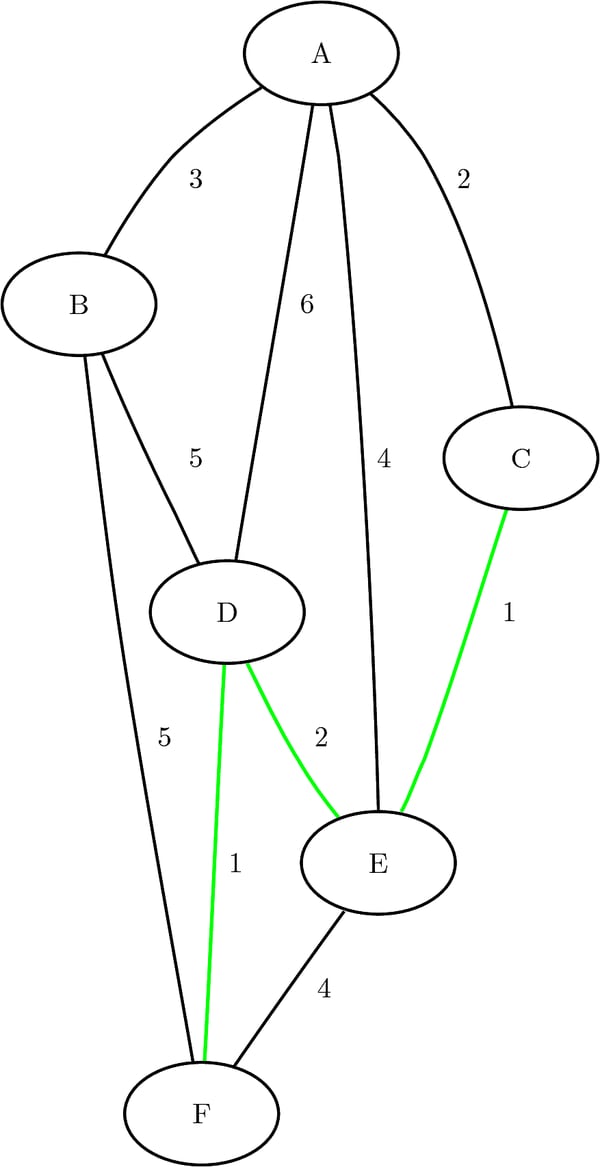
This example illustrates the use of the shortest path algorithm for all source-sink pairs on the simple undirected graph G shown in Figure 2.53.

Figure 2.53: A Simple Undirected Graph G

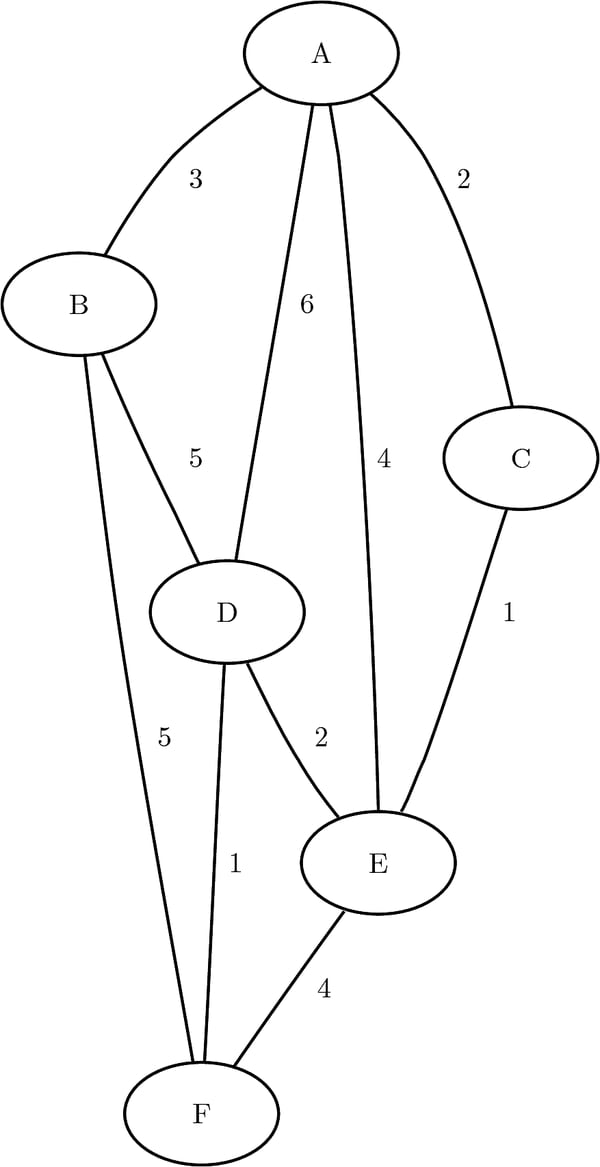
The undirected graph G can be represented by the following links data set, LinkSetIn:

data LinkSetIn;
   input from $ to $ weight @@;
   datalines;
A B 3  A C 2  A D 6  A E 4  B D 5
B F 5  C E 1  D E 2  D F 1  E F 4
;

The following statements calculate shortest paths for all source-sink pairs:

proc optnet
   data_links     = LinkSetIn;
   shortpath
      out_weights = ShortPathW
      out_paths   = ShortPathP;
run;

The data set ShortPathP contains the shortest paths and is shown in Figure 2.54.

Figure 2.54: All-Pairs Shortest Paths

source	sink	order	from	to	weight
A	B	1	A	B	3
A	C	1	A	C	2
A	D	1	A	C	2
A	D	2	C	E	1
A	D	3	E	D	2
A	E	1	A	C	2
A	E	2	C	E	1
A	F	1	A	C	2
A	F	2	C	E	1
A	F	3	E	D	2
A	F	4	D	F	1
B	A	1	B	A	3
B	C	1	B	A	3
B	C	2	A	C	2
B	D	1	B	D	5
B	E	1	B	A	3
B	E	2	A	C	2
B	E	3	C	E	1
B	F	1	B	F	5
C	A	1	C	A	2
C	B	1	C	A	2
C	B	2	A	B	3
C	D	1	C	E	1
C	D	2	E	D	2
C	E	1	C	E	1
C	F	1	C	E	1
C	F	2	E	D	2
C	F	3	D	F	1
D	A	1	D	E	2
D	A	2	E	C	1
D	A	3	C	A	2
D	B	1	D	B	5
D	C	1	D	E	2
D	C	2	E	C	1
D	E	1	D	E	2
D	F	1	D	F	1
E	A	1	E	C	1
E	A	2	C	A	2
E	B	1	E	C	1
E	B	2	C	A	2
E	B	3	A	B	3
E	C	1	E	C	1
E	D	1	E	D	2
E	F	1	E	D	2
E	F	2	D	F	1
F	A	1	F	D	1
F	A	2	D	E	2
F	A	3	E	C	1
F	A	4	C	A	2
F	B	1	F	B	5
F	C	1	F	D	1
F	C	2	D	E	2
F	C	3	E	C	1
F	D	1	F	D	1
F	E	1	F	D	1
F	E	2	D	E	2

The data set ShortPathW contains the path weight for the shortest paths of each source-sink pair and is shown in Figure 2.55.

Figure 2.55: All-Pairs Shortest Paths Summary

source	sink	path_weight
A	B	3
A	C	2
A	D	5
A	E	3
A	F	6
B	A	3
B	C	5
B	D	5
B	E	6
B	F	5
C	A	2
C	B	5
C	D	3
C	E	1
C	F	4
D	A	5
D	B	5
D	C	3
D	E	2
D	F	1
E	A	3
E	B	6
E	C	1
E	D	2
E	F	3
F	A	6
F	B	5
F	C	4
F	D	1
F	E	3

When you are interested only in the source-sink pair that has the longest shortest path, you can use the PATHS= option. This option affects only the output processing; it does not affect the computation. All the designated source-sink shortest paths are calculated, but only the longest ones are written to the output data set.

The following statements display only the longest shortest paths:

proc optnet
   data_links   = LinkSetIn;
   shortpath
      paths     = longest
      out_paths = ShortPathLong;
run;

The data set ShortPathLong now contains the longest shortest paths and is shown in Figure 2.56.

Figure 2.56: Longest Shortest Paths

source	sink	order	from	to	weight
A	F	1	A	C	2
A	F	2	C	E	1
A	F	3	E	D	2
A	F	4	D	F	1
B	E	1	B	A	3
B	E	2	A	C	2
B	E	3	C	E	1
E	B	1	E	C	1
E	B	2	C	A	2
E	B	3	A	B	3
F	A	1	F	D	1
F	A	2	D	E	2
F	A	3	E	C	1
F	A	4	C	A	2

Shortest Paths for a Subset of Source-Sink Pairs

This section illustrates the use of a node subset data set, the DATA_NODES_SUB= option, and the shortest path algorithm to calculate shortest paths for a subset of source-sink pairs. The data set variables source and sink are used as indicators to specify which pairs to process. The marked source nodes define a set S, and the marked sink nodes define a set T. PROC OPTNET then calculates all the source-sink pairs in the crossproduct of these two sets.

For example, the following DATA step tells PROC OPTNET to calculate the pairs in 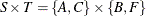$S\times T=\{ A,C\} \times \{ B,F\}$ :

data NodeSubSetIn;
   input node $ source sink;
   datalines;
A 1 0
C 1 0
B 0 1
F 0 1
;

The following statements calculate a shortest path for the four combinations of source-sink pairs:

proc optnet
   data_nodes_sub = NodeSubSetIn
   data_links     = LinkSetIn;
   shortpath
      out_paths   = ShortPath;
run;

The data set ShortPath contains the shortest paths and is shown in Figure 2.57.

Figure 2.57: Shortest Paths for a Subset of Source-Sink Pairs

source	sink	order	from	to	weight
A	B	1	A	B	3
A	F	1	A	C	2
A	F	2	C	E	1
A	F	3	E	D	2
A	F	4	D	F	1
C	B	1	C	A	2
C	B	2	A	B	3
C	F	1	C	E	1
C	F	2	E	D	2
C	F	3	D	F	1

Shortest Paths for a Subset of Source or Sink Pairs

This section illustrates the use of the shortest path algorithm to calculate shortest paths between a subset of source (or sink) nodes and all other sink (or source) nodes.

In this case, you designate the subset of source (or sink) nodes in the node subset data set by specifying the source (or sink). By specifying only one of the variables, you indicate that you want PROC OPTNET to calculate all pairs from a subset of source nodes (or to calculate all pairs to a subset of sink nodes).

For example, the following DATA step designates nodes B and E as source nodes:

data NodeSubSetIn;
   input node $ source;
   datalines;
B 1
E 1
;

You can use the same PROC OPTNET call as is used in the section Shortest Paths for a Subset of Source-Sink Pairs to calculate all the shortest paths from nodes B and E. The data set ShortPath contains the shortest paths and is shown in Figure 2.58.

Figure 2.58: Shortest Paths for a Subset of Source Pairs

source	sink	order	from	to	weight
B	A	1	B	A	3
B	C	1	B	A	3
B	C	2	A	C	2
B	D	1	B	D	5
B	E	1	B	A	3
B	E	2	A	C	2
B	E	3	C	E	1
B	F	1	B	F	5
E	A	1	E	C	1
E	A	2	C	A	2
E	B	1	E	C	1
E	B	2	C	A	2
E	B	3	A	B	3
E	C	1	E	C	1
E	D	1	E	D	2
E	F	1	E	D	2
E	F	2	D	F	1

Conversely, the following DATA step designates nodes B and E as sink nodes:

data NodeSubSetIn;
   input node $ sink;
   datalines;
B 1
E 1
;

You can use the same PROC OPTNET call again to calculate all the shortest paths to nodes B and E. The data set ShortPath contains the shortest paths and is shown in Figure 2.59.

Figure 2.59: Shortest Paths for a Subset of Sink Pairs

source	sink	order	from	to	weight
A	B	1	A	B	3
A	E	1	A	C	2
A	E	2	C	E	1
B	E	1	B	A	3
B	E	2	A	C	2
B	E	3	C	E	1
C	B	1	C	A	2
C	B	2	A	B	3
C	E	1	C	E	1
D	B	1	D	B	5
D	E	1	D	E	2
E	B	1	E	C	1
E	B	2	C	A	2
E	B	3	A	B	3
F	B	1	F	B	5
F	E	1	F	D	1
F	E	2	D	E	2

Shortest Paths for One Source-Sink Pair

This section illustrates the use of the shortest path algorithm to calculate shortest paths between one source-sink pair by using the SOURCE= and SINK= options.

The following statements calculate a shortest path between node C and node F:

proc optnet
   data_links   = LinkSetIn;
   shortpath
      source    = C
      sink      = F
      out_paths = ShortPath;
run;

The data set ShortPath contains this shortest path and is shown in Figure 2.60.

Figure 2.60: Shortest Paths for One Source-Sink Pair

source	sink	order	from	to	weight
C	F	1	C	E	1
C	F	2	E	D	2
C	F	3	D	F	1

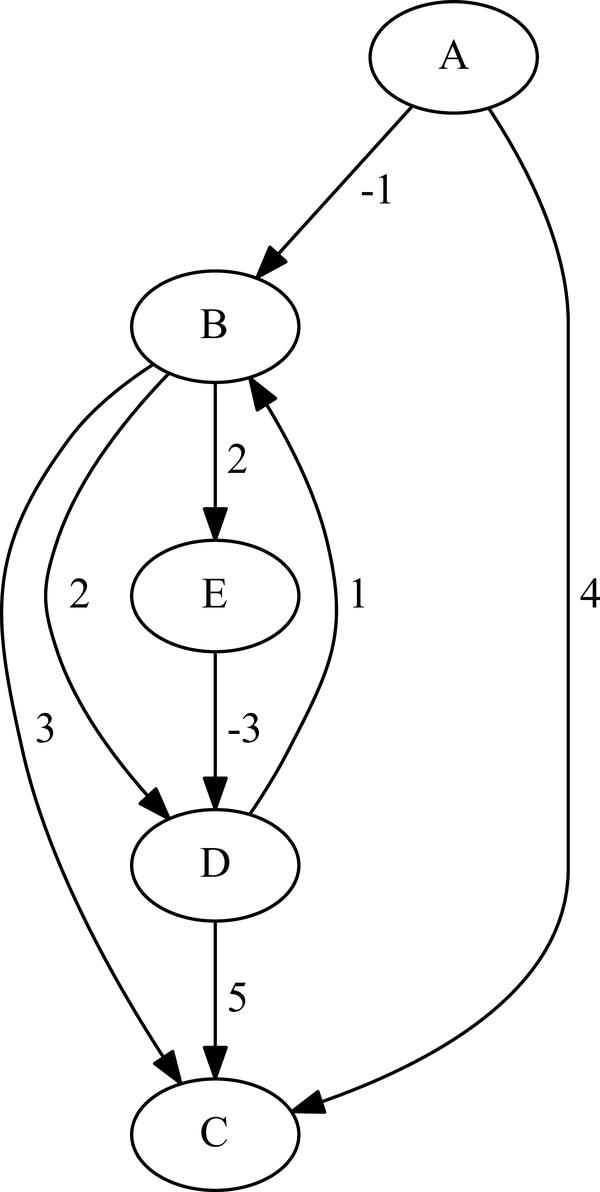
The shortest path is shown graphically in Figure 2.61.

Figure 2.61: Shortest Path between Nodes C and F

Shortest Paths with Auxiliary Weight Calculation

This section illustrates the use of the shortest path algorithm with auxiliary weights to calculate the shortest paths between all source-sink pairs.

Consider a links data set in which the auxiliary weight is a counter for each link:

data LinkSetIn;
   input from $ to $ weight count @@;
   datalines;
A B 3 1  A C 2 1  A D 6 1  A E 4 1  B D 5 1
B F 5 1  C E 1 1  D E 2 1  D F 1 1  E F 4 1
;

The following statements calculate shortest paths for all source-sink pairs:

proc optnet
   data_links     = LinkSetIn;
   shortpath
      weight2     = count
      out_weights = ShortPathW;
run;

The data set ShortPathW contains the total path weight for shortest paths in each source-sink pair and is shown in Figure 2.62. Because the variable count in LinkSetIn has a value of 1 for all links, the value in the output data set variable path_weights2 contains the number of links in each shortest path.

Figure 2.62: Shortest Paths Including Auxiliary Weights in Calculation

source	sink	path_weight	path_weight2
A	B	3	1
A	C	2	1
A	D	5	3
A	E	3	2
A	F	6	4
B	A	3	1
B	C	5	2
B	D	5	1
B	E	6	3
B	F	5	1
C	A	2	1
C	B	5	2
C	D	3	2
C	E	1	1
C	F	4	3
D	A	5	3
D	B	5	1
D	C	3	2
D	E	2	1
D	F	1	1
E	A	3	2
E	B	6	3
E	C	1	1
E	D	2	1
E	F	3	2
F	A	6	4
F	B	5	1
F	C	4	3
F	D	1	1
F	E	3	2

The section Road Network Shortest Path shows an example of using the shortest path algorithm to minimize travel to and from work based on traffic conditions.

Shortest Paths with Negative Link Weights

This section illustrates the use of the shortest path algorithm on a simple directed graph G with negative link weights, shown in Figure 2.63.

Figure 2.63: A Simple Directed Graph G with Negative Link Weights

A Simple Directed Graph with Negative Link Weights

You can represent the directed graph G by using the following links data set LinkSetIn:

data LinkSetIn;
   input from $ to $ weight @@;
   datalines;
A B -1  A C  4  B C  3  B D  2  B E  2
D B  1  D C  5  E D -3
;

The following statements calculate the shortest paths between source node E and sink node B:

proc optnet
   direction      = directed
   data_links     = LinkSetIn;
   shortpath
      source      = E
      sink        = B
      out_paths   = ShortPathP;
run;

The data set ShortPathP contains the shortest path from node E to node B and is shown in Figure 2.64.

Figure 2.64: Shortest Paths with Negative Link Weights

source	sink	order	from	to	weight
E	B	1	E	D	-3
E	B	2	D	B	1

Now, consider the following adjustment to the weight of link 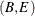$(B,E)$ :

data LinkSetIn;
   set LinkSetIn;
   if(from="B" and to="E") then
      weight=1;
run;

In this case, there is a negative weight cycle (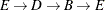 $E \rightarrow D \rightarrow B \rightarrow E$ ). The Bellman-Ford algorithm catches this and produces an error, as shown in Figure 2.65.