The Network Solver
- Overview
- Getting Started
-
Syntax

-
Details
 Input Data for the Network SolverSolving over Subsets of Nodes and Links (Filters)Numeric LimitationsBiconnected Components and Articulation PointsCliqueConnected ComponentsCycleLinear Assignment (Matching)Minimum-Cost Network FlowMinimum CutMinimum Spanning TreeShortest PathTransitive ClosureTraveling Salesman ProblemMacro Variable _OROPTMODEL_
Input Data for the Network SolverSolving over Subsets of Nodes and Links (Filters)Numeric LimitationsBiconnected Components and Articulation PointsCliqueConnected ComponentsCycleLinear Assignment (Matching)Minimum-Cost Network FlowMinimum CutMinimum Spanning TreeShortest PathTransitive ClosureTraveling Salesman ProblemMacro Variable _OROPTMODEL_ -
Examples
 Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities
Articulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities - References
Linear Assignment (Matching)
The linear assignment problem (LAP) is a fundamental problem in combinatorial optimization that involves assigning workers to tasks at minimal costs. In graph theoretic terms, the LAP is equivalent to finding a minimum-weight matching in a weighted bipartite directed graph. In a bipartite graph, the nodes can be divided into two disjoint sets S (workers) and T (tasks) such that every link connects a node in S to a node in T. That is, the node sets S and T are independent. The concept of assigning workers to tasks can be generalized to the assignment of any abstract object from one group to some abstract object from a second group.
The linear assignment problem can be formulated as an integer programming optimization problem. The form of the problem depends
on the sizes of the two input sets, S and T. Let A represent the set of possible assignments between sets S and T. In the bipartite graph, these assignments are the links. If 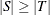 , then the following optimization problem is solved:
, then the following optimization problem is solved:
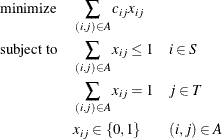
This model allows for some elements of set S (workers) to go unassigned (if 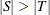 ).
).
If 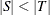 , then the following optimization problem is solved:
, then the following optimization problem is solved:
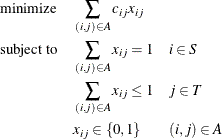
This model allows for some elements of set T (tasks) to go unassigned.
In the network solver, you can invoke the linear assignment problem solver by using the LINEAR_ASSIGNMENT option. The algorithm that the network solver uses for solving a LAP is based on augmentation of shortest paths (Jonker and Volgenant 1987). This algorithm can be applied as long as the graph is bipartite.
The resulting assignment (or matching) is contained in the set that is specified in the ASSIGNMENTS= suboption of the OUT= option.
For a detailed example, see Example 9.3: Linear Assignment Problem for Minimizing Swim Times.