The Network Solver

Algorithm Options

BICONCOMP<=() >

finds biconnected components and articulation points of an undirected input graph. For more information, see the section Biconnected Components and Articulation Points.

CLIQUE<=( suboption ) >

finds maximal cliques in the input graph. For more information, see the section Clique.

You can specify the following suboption:

MAXCLIQUES=number: specifies the maximum number of cliques to return. The default is the positive number that has the largest absolute value that can be represented in your operating environment.

CONCOMP<=( suboption ) >

finds the connected components of the input graph. For more information, see the section Connected Components.

You can specify the following suboption:

ALGORITHM=DFS | UNION_FIND

specifies the algorithm to use for calculating connected components. Table 9.8 describes the valid values for this option.

Table 9.8: Values for the ALGORITHM= Option

Option Value	Description
DFS	Uses the depth-first search algorithm for connected components.
UNION_FIND	Uses the union-find algorithm for connected components. You can use ALGORITHM=UNION_FIND only with undirected graphs.

By default, ALGORITHM=UNION_FIND for undirected graphs, and ALGORITHM=DFS for directed graphs.

CYCLE<=( suboptions ) >

finds the cycles (or the existence of a cycle) in the input graph. For more information, see the section Cycle.

You can specify the following suboptions in the CYCLE= option:

MAXCYCLES=number

specifies the maximum number of cycles to return. The default is the positive number that has the largest absolute value that can be represented in your operating environment. This option works only when you also specify MODE=ALL_CYCLES.

MAXLENGTH=number

specifies the maximum number of links to allow in a cycle. Any cycle whose length is greater than number is removed from the results. The default is the positive number that has the largest absolute value that can be represented in your operating environment. By default, nothing is removed from the results. This option works only when you also specify MODE=ALL_CYCLES.

MAXLINKWEIGHT=number

specifies the maximum sum of link weights to allow in a cycle. Any cycle whose sum of link weights is greater than number is removed from the results. The default is the positive number that has the largest absolute value that can be represented in your operating environment. By default, nothing is filtered. This option works only when you also specify MODE=ALL_CYCLES.

MAXNODEWEIGHT=number

specifies the maximum sum of node weights to allow in a cycle. Any cycle whose sum of node weights is greater than number is removed from the results. The default is the positive number that has the largest absolute value that can be represented in your operating environment. By default, nothing is filtered. This option works only when you also specify MODE=ALL_CYCLES.

MINLENGTH=number

specifies the minimum number of links to allow in a cycle. Any cycle that has fewer links than number is removed from the results. The default is 1. By default, only self-loops are filtered. This option works only when you also specify MODE=ALL_CYCLES.

MINLINKWEIGHT=number

specifies the minimum sum of link weights to allow in a cycle. Any cycle whose sum of link weights is less than number is removed from the results. The default the negative number that has the largest absolute value that can be represented in your operating environment. By default, nothing is filtered. This option works only when you also specify MODE=ALL_CYCLES.

MINNODEWEIGHT=number

specifies the minimum sum of node weights to allow in a cycle. Any cycle whose sum of node weights is less than number is removed from the results. The default is the negative number that has the largest absolute value that can be represented in your operating environment. By default, nothing is filtered. This option works only when you also specify MODE=ALL_CYCLES.

MODE=ALL_CYCLES | FIRST_CYCLE

specifies whether to stop after finding the first cycle. Table 9.9 describes the valid values for this option.

Table 9.9: Values for the MODE= Option

Option Value	Description
ALL_CYCLES	Returns all (unique, elementary) cycles found.
FIRST_CYCLE	Returns the first cycle found.

By default, MODE=FIRST_CYCLE.

LINEAR_ASSIGNMENT<=() > LAP<=() >

solves the minimal-cost linear assignment problem. In graph terms, this problem is also known as the minimum link-weighted matching problem on a bipartite directed graph. The input data (the cost matrix) is defined as a directed graph by specifying the LINKS= option in the SOLVE WITH NETWORK statement, where the costs are defined as link weights. Internally, the graph is treated as a bipartite directed graph.

For more information, see the section Linear Assignment (Matching).

MINCOSTFLOW<=() > MCF<=() >

solves the minimum-cost network flow problem.

For more information, see the section Minimum-Cost Network Flow.

MINCUT<=( suboptions ) >

finds the minimum link-weighted cut of an input graph. For more information, see the section Minimum Cut. You can specify the following suboptions in the MINCUT= option:

MAXNUMCUTS=number: specifies the maximum number of cuts to return from the algorithm. The minimal cut and any others found during the search, up to number, are returned. By default, MAXNUMCUTS=1.
MAXWEIGHT=number: specifies the maximum weight of the cuts to return from the algorithm. Only cuts that have weight less than or equal to number are returned. The default is the positive number that has the largest absolute value that can be represented in your operating environment.

MINSPANTREE<=() > MST<=() >

solves the minimum link-weighted spanning tree problem on an input graph. For more information, see the section Minimum Spanning Tree.

SHORTPATH<=( suboptions ) >

calculates shortest paths between sets of nodes on the input graph. For more information, see the section Shortest Path.

You can specify the following suboptions:

PATHS=ALL | LONGEST | SHORTEST

specifies the type of output for shortest paths results.

Table 9.10 lists the valid values for this suboption.

Table 9.10: Values for the PATHS= Option

Option Value	Description
ALL	Outputs shortest paths for all pairs of source-sinks.
LONGEST	Outputs shortest paths for the source-sink pair that has the longest (finite) length. If other source-sink pairs (up to 100) have equally long length, they are also output.
SHORTEST	Outputs shortest paths for the source-sink pair that has the shortest length. If other source-sink pairs (up to 100) have equally short length, they are also output.

By default, SHORTPATH=ALL.

SINK=set-name

specifies the set of sink nodes.

SOURCE=set-name

specifies the set of source nodes.

USEWEIGHT=YES | NO

specifies whether to use weights in calculating shortest paths as listed in Table 9.11.

Table 9.11: Values for USEWEIGHT= Option

Option Value	Description
YES	Uses weights (if they exist) in shortest path calculations.
NO	Does not use weights in shortest path calculations.

By default, USEWEIGHT=YES.

TRANSITIVE_CLOSURE<=() > TRANSCL<=() >

calculates the transitive closure of an input graph. For more information, see the section Transitive Closure.

TSP<=( suboptions ) >

solves the traveling salesman problem. For more information, see the section Traveling Salesman Problem.

The algorithm that is used to solve this problem is built around the same method as is used in PROC OPTMILP: a branch-and-cut algorithm. Many of the following suboptions are the same as those described for the OPTMILP procedure in the SAS/OR User's Guide: Mathematical Programming.

You can specify the following suboptions:

ABSOBJGAP=number

specifies a stopping criterion. When the absolute difference between the best integer objective and the objective of the best remaining branch-and-bound node becomes less than the value of number, the solver stops. The value of number can be any nonnegative number. By default, ABSOBJGAP=1E–6.

CONFLICTSEARCH=number | string

specifies the level of conflict search that the network solver performs. The solver performs a conflict search to find clauses that result from infeasible subproblems that arise in the search tree. Table 9.12 describes the valid values for this option.

Table 9.12: Values for CONFLICTSEARCH= Option

number	string	Description
–1	AUTOMATIC	Performs a conflict search based on a strategy that is determined by the network solver
0	NONE	Disables conflict search
1	MODERATE	Performs a moderate conflict search
2	AGGRESSIVE	Performs an aggressive conflict search

By default, CONFLICTSEARCH=AUTOMATIC.

CUTOFF=number

cuts off any branch-and-bound nodes in a minimization problem that has an objective value that is greater than number. The value of number can be any number.

The default value is the positive number that has the largest absolute value that can be represented in your operating environment.

CUTSTRATEGY=number | string

specifies the level of cutting planes to be generated by the network solver. TSP-specific cutting planes are always generated. Table 9.13 describes the valid values for this option.

Table 9.13: Values for CUTSTRATEGY= Option

number	string	Description
–1	AUTOMATIC	Generates cutting planes based on a strategy determined by the mixed integer linear programming solver
0	NONE	Disables generation of mixed integer programming cutting planes (some TSP-specific cutting planes are still active for validity)
1	MODERATE	Uses a moderate cut strategy
2	AGGRESSIVE	Uses an aggressive cut strategy

By default, CUTSTRATEGY=NONE.

EMPHASIS=number | string

specifies a search emphasis option. Table 9.14 describes the valid values for this option.

Table 9.14: Values for EMPHASIS= Option

number	string	Description
0	BALANCE	Performs a balanced search
1	OPTIMAL	Emphasizes optimality over feasibility
2	FEASIBLE	Emphasizes feasibility over optimality

By default, EMPHASIS=BALANCE.

HEURISTICS=number | string

controls the level of initial and primal heuristics that the network solver applies. This level determines how frequently the network solver applies primal heuristics during the branch-and-bound tree search. It also affects the maximum number of iterations that are allowed in iterative heuristics. Some computationally expensive heuristics might be disabled by the solver at less aggressive levels. Table 9.15 lists the valid values for this option.

Table 9.15: Values for HEURISTICS= Option

number	string	Description
–1	AUTOMATIC	Applies the default level of heuristics
0	NONE	Disables all initial and primal heuristics
1	BASIC	Applies basic initial and primal heuristics at low frequency
2	MODERATE	Applies most initial and primal heuristics at moderate frequency
3	AGGRESSIVE	Applies all initial primal heuristics at high frequency

By default, HEURISTICS=AUTOMATIC.

MAXNODES=number

specifies the maximum number of branch-and-bound nodes to be processed. The value of number can be any nonnegative integer up to the largest four-byte signed integer, which is $2^{31} - 1$ .

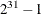By default, MAXNODES= $2^{31} - 1$ .

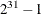MAXSOLS=number

specifies the maximum number of feasible tours to be identified. If number solutions have been found, then the solver stops. The value of number can be any positive integer up to the largest four-byte signed integer, which is $2^{31} - 1$ .

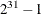By default, MAXSOLS= $2^{31} - 1$ .

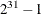MILP=number | string

specifies whether to use a mixed integer linear programming (MILP) solver for solving the traveling salesman problem. The MILP solver attempts to find the overall best TSP tour by using a branch-and-bound based algorithm. This algorithm can be expensive for large-scale problems. If MILP=OFF, then the network solver uses its initial heuristics to find a feasible, but not necessarily optimal, tour as quickly as possible. Table 9.16 describes the valid values for this option.

Table 9.16: Values for MILP= Option

number	string	Description
1	ON	Uses a mixed integer linear programming solver
0	OFF	Does not use a mixed integer linear programming solver

By default, MILP=ON

NODESEL=number | string

specifies the branch-and-bound node selection strategy option. For more information about node selection, see Chapter 13: The OPTMILP Procedure. Table 9.17 describes the valid values for this option.

Table 9.17: Values for NODESEL= Option

number	string	Description
–1	AUTOMATIC	Uses automatic node selection
0	BESTBOUND	Chooses the node that has the best relaxed objective (best-bound-first strategy)
1	BESTESTIMATE	Chooses the node that has the best estimate of the integer objective value (best-estimate-first strategy)
2	DEPTH	Chooses the most recently created node (depth-first strategy)

By default, NODESEL=AUTOMATIC.

PROBE=number | string

specifies a probing option. Table 9.18 describes the valid values for this option.

Table 9.18: Values for PROBE= Option

number	string	Description
–1	AUTOMATIC	Uses an automatic probing strategy
0	NONE	Disables probing
1	MODERATE	Uses the probing moderately
2	AGGRESSIVE	Uses the probing aggressively

By default, PROBE=NONE.

RELOBJGAP=number

specifies a stopping criterion that is based on the best integer objective (BestInteger) and the objective of the best remaining node (BestBound). The relative objective gap is equal to

$\mid \mbox{BestInteger} - \mbox{BestBound}\mid / \left(\mbox{1E--10}~ + \mid \mbox{BestBound}\mid \right)$

When this value becomes less than the specified gap size number, the solver stops. The value of number can be any nonnegative number.

By default, RELOBJGAP=1E–4.

STRONGITER=number | AUTOMATIC

specifies the number of simplex iterations that the network solver performs for each variable in the candidate list when it uses the strong branching variable selection strategy. The value of number can be any positive integer up to the largest four-byte signed integer, which is 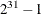$2^{31} - 1$ . If you specify the keyword AUTOMATIC or the value –1, the network solver uses the default value, which it calculates automatically.

STRONGLEN=number | AUTOMATIC

specifies the number of candidates that the network solver considers when it uses the strong branching variable selection strategy. The value of number can be any positive integer up to the largest four-byte signed integer, which is 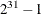$2^{31} - 1$ . If you specify the keyword AUTOMATIC or the value –1, the network solver uses the default value, which it calculates automatically.

TARGET=number

specifies a stopping criterion for minimization problems. If the best integer objective is better than or equal to number, the solver stops. The value of number can be any number.

By default, TARGET is the negative number that has the largest absolute value that can be represented in your operating environment.

VARSEL=number | string

specifies the rule for selecting the branching variable. For more information about variable selection, see Chapter 13: The OPTMILP Procedure. Table 9.19 describes the valid values for this option.

Table 9.19: Values for VARSEL= Option

number	string	Description
–1	AUTOMATIC	Uses automatic branching variable selection
0	MAXINFEAS	Chooses the variable that has maximum infeasibility
1	MININFEAS	Chooses the variable that has minimum infeasibility
2	PSEUDO	Chooses a branching variable based on pseudocost
3	STRONG	Uses the strong branching variable selection strategy

By default, VARSEL=AUTOMATIC.