The Decomposition Algorithm

Example 14.7 Vehicle Routing Problem

The vehicle routing problem (VRP) finds a minimum-cost routing of a fixed number of vehicles to service the demands of a set of customers. Define a set $C = \{ 2,\dots ,|C|+1\}$ of customers, and a demand, $d_ c$ , at each customer $c$ . Let $N=C \cup \{ 1\}$ be the set of nodes, including the vehicle depot, which are designated as node $i=1$ . Let $A=N \times N$ be the set of arcs, $V$ be the set of vehicles (each of which has capacity $L$ ), and $c_{ij}$ be the travel time from node $i$ to node $j$ .

Let $y_{ik}$ be a binary variable, which, if set to $1$ , indicates that node $i$ is visited by vehicle $k$ . Let $z_{ijk}$ be a binary variable, which, if set to $1$ , indicates that arc $(i,j)$ is traversed by vehicle $k$ , and let $x_{ijk}$ be a continuous variable that denotes the amount of product (flow) on arc $(i,j)$ that is carried by vehicle $k$ .

A VRP can be formulated as a MILP as follows:

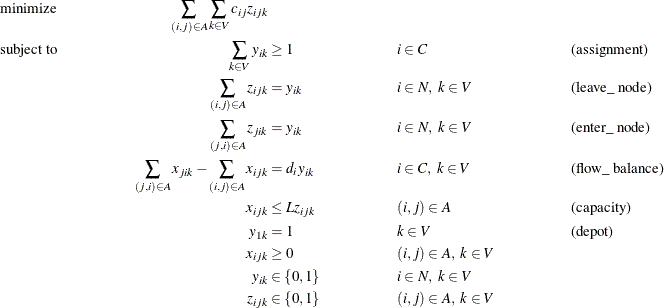
$\begin{align*} & \text {minimize} & \sum _{(i,j) \in A} \sum _{k \in V} c_{ij} z_{ijk}\\ & \text {subject to} & \sum _{k \in V} y_{ik} & \geq 1 & & i \in C & & \text {(assignment)}\\ & & \sum _{(i,j) \in A} z_{ijk} & = y_{ik} & & i \in N, \ k \in V & & \text {(leave\_ node)} \\ & & \sum _{(j,i) \in A} z_{jik} & = y_{ik} & & i \in N, \ k \in V & & \text {(enter\_ node)} \\ & & \sum _{(j,i) \in A} x_{jik} - \sum _{(i,j) \in A} x_{ijk} & = d_ i y_{ik} & & i \in C, \ k \in V & & \text {(flow\_ balance)}\\ & & x_{ijk} & \leq L z_{ijk} & & (i,j) \in A & & \text {(capacity)} \\ & & y_{1k} & = 1 & & k \in V & & \text {(depot)} \\ & & x_{ijk} & \geq 0 & & (i,j) \in A, \ k \in V \\ & & y_{ik} & \in \left\{ 0,1\right\} & & i \in N, \ k \in V \\ & & z_{ijk} & \in \left\{ 0,1\right\} & & (i,j) \in A, \ k \in V \end{align*}$

In this formulation, constraints (assignment) ensure that each customer is serviced by at least one vehicle. The objective function ensures that there exists an optimal solution that never assigns a customer to more than one vehicle. Constraints (leave_node) and (enter_node) enforce the condition that if node $i$ is visited by vehicle $k$ , then vehicle $k$ must use exactly one arc that enters node $i$ and one arc that leaves node $i$ . Conversely, if node $i$ is not visited by vehicle $k$ , then no arcs that enter or leave node $i$ can be used by vehicle $k$ . Constraints (flow_balance) define flow conservation at each node for each vehicle. That is, if a node $i$ is visited by vehicle $k$ , then the amount of product from vehicle $k$ that enters and leaves that node must equal the demand at that node. Conversely, if node $i$ is not visited by vehicle $k$ , then the amount of product from vehicle $k$ that enters and leaves that node must be 0. Constraints (capacity) enforce the amount of product in each vehicle to be always less than or equal to the vehicle capacity $L$ . Finally, constraints (depot) enforce that each vehicle must start and end at the depot node.

In this formulation, the vehicle identifier is arbitrary. Consider a decomposition by vehicle, where assignment constraints form the master problem and all other constraints form identical routing subproblems. As described in the section Special Case: Identical Blocks, this is a situation in which an aggregate formulation and Ryan-Foster branching can greatly improve performance by reducing symmetry.

VRPLIB, located at http://www.coin-or.org/SYMPHONY/branchandcut/VRP/data/index.htm, is a set of benchmark instances for the VRP. The following data set vrpdata represents an instance from VRPLIB with 22 nodes and 8 vehicles (P-n22-k8.vrp), which was originally described in Augerat et al. (1995). The data set lists each node, its coordinates and its demand.

/* number of vehicles available */
%let num_vehicles = 8;
/* capacity for each vehicle */
%let capacity = 3000;
/* node, x coordinate, y coordinate, demand */
data vrpdata;
   input node x y demand;
   datalines;
1  145 215    0
2  151 264 1100
3  159 261  700
4  130 254  800
5  128 252 1400
6  163 247 2100
7  146 246  400
8  161 242  800
9  142 239  100
10 163 236  500
11 148 232  600
12 128 231 1200
13 156 217 1300
14 129 214 1300
15 146 208  300
16 164 208  900
17 141 206 2100
18 147 193 1000
19 164 193  900
20 129 189 2500
21 155 185 1800
22 139 182  700
;

The following PROC OPTMODEL statements read in the data, declare the optimization model, and use the decomposition algorithm to solve it:

proc optmodel;
   /* read the node location and demand data */
   set NODES;
   num x {NODES};
   num y {NODES};
   num demand {NODES};
   num capacity = &capacity;
   num num_vehicles = &num_vehicles;
   read data vrpdata into NODES=[node] x y demand;
   set ARCS = {i in NODES, j in NODES: i ne j};
   set VEHICLES = 1..num_vehicles;

   /* define the depot as node 1 */
   num depot = 1;

   /* define the arc cost as the rounded Euclidean distance */
   num cost {<i,j> in ARCS} = round(sqrt((x[i]-x[j])^2 + (y[i]-y[j])^2));

   /* Flow[i,j,k] is the amount of demand carried on arc (i,j) by vehicle k */
   var Flow {ARCS, VEHICLES} >= 0 <= capacity;
   /* UseNode[i,k] = 1, if and only if node i is serviced by vehicle k */
   var UseNode {NODES, VEHICLES} binary;
   /* UseArc[i,j,k] = 1, if and only if arc (i,j) is traversed by vehicle k */
   var UseArc {ARCS, VEHICLES} binary;

   /* minimize the total distance traversed */
   min TotalCost = sum {<i,j> in ARCS, k in VEHICLES} cost[i,j] * UseArc[i,j,k];

   /* each non-depot node must be serviced by at least one vehicle */
   con Assignment {i in NODES diff {depot}}:
      sum {k in VEHICLES} UseNode[i,k] >= 1;

   /* each vehicle must start at the depot node */
   for{k in VEHICLES} fix UseNode[depot,k] = 1;

   /* some vehicle k traverses an arc which leaves node i
      if and only if UseNode[i,k] = 1 */
   con LeaveNode {i in NODES, k in VEHICLES}:
      sum {<(i),j> in ARCS} UseArc[i,j,k] = UseNode[i,k];

   /* some vehicle k traverses an arc which enters node i
      if and only if UseNode[i,k] = 1 */
   con EnterNode {i in NODES, k in VEHICLES}:
      sum {<j,(i)> in ARCS} UseArc[j,i,k] = UseNode[i,k];

   /* the amount of demand supplied by vehicle k to node i must equal demand
      if UseNode[i,k] = 1; otherwise, it must equal 0 */
   con FlowBalance {i in NODES diff {depot}, k in VEHICLES}:
       sum {<j,(i)> in ARCS} Flow[j,i,k] - sum {<(i),j> in ARCS} Flow[i,j,k]
       = demand[i] * UseNode[i,k];

   /* if UseArc[i,j,k] = 1, then the flow on arc (i,j) must be at most capacity
      if UseArc[i,j,k] = 0, then no flow is allowed on arc (i,j) */
   con VehicleCapacity {<i,j> in ARCS, k in VEHICLES}:
      Flow[i,j,k] <= Flow[i,j,k].ub * UseArc[i,j,k];

   /* decomp by vehicle */
   for {i in NODES, k in VEHICLES} do;
      LeaveNode[i,k].block = k;
      EnterNode[i,k].block = k;
   end;
   for {i in NODES diff {depot}, k in VEHICLES} FlowBalance[i,k].block = k;
   for {<i,j> in ARCS, k in VEHICLES} VehicleCapacity[i,j,k].block = k;

   /* solve using decomp (aggregate formulation) */
   solve with MILP / decomp=(logfreq=20);

The following OPTMODEL statements create node and edge data for the optimal routing:

   /* create solution data set */
   str color {k in VEHICLES} =
      ['red' 'green' 'blue' 'black' 'orange' 'gray' 'maroon' 'purple'];
   create data node_data from [i] x y;
   create data edge_data from [i j k]=
      {<i,j> in ARCS, k in VEHICLES: UseArc[i,j,k].sol > 0.5}
      x1=x[i] y1=y[i] x2=x[j] y2=y[j] linecolor=color[k];
quit;

The solution summary is displayed in Output 14.7.1.

Output 14.7.1: Solution Summary

The OPTMODEL Procedure

Solution Summary
Solver	MILP
Algorithm	Decomposition
Objective Function	TotalCost
Solution Status	Optimal
Objective Value	603

Relative Gap	0
Absolute Gap	0
Primal Infeasibility	0
Bound Infeasibility	0
Integer Infeasibility	0

Best Bound	603
Nodes	1
Iterations	69
Presolve Time	0.14
Solution Time	175.02

The iteration log is displayed in Output 14.7.2.

Output 14.7.2: Log

NOTE: There were 22 observations read from the data set WORK.VRPDATA.

NOTE: Problem generation will use 4 threads.

NOTE: The problem has 7568 variables (0 free, 8 fixed).

NOTE: The problem has 3872 binary and 0 integer variables.

NOTE: The problem has 4237 linear constraints (3696 LE, 520 EQ, 21 GE, 0 range).

NOTE: The problem has 22528 linear constraint coefficients.

NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).

NOTE: The MILP presolver value AUTOMATIC is applied.

NOTE: The MILP presolver removed 8 variables and 0 constraints.

NOTE: The MILP presolver removed 16 constraint coefficients.

NOTE: The MILP presolver modified 0 constraint coefficients.

NOTE: The presolved problem has 7560 variables, 4237 constraints, and 22512

constraint coefficients.

NOTE: The MILP solver is called.

NOTE: The Decomposition algorithm is used.

NOTE: The Decomposition algorithm is executing in single-machine mode.

NOTE: The DECOMP method value USER is applied.

NOTE: All blocks are identical.

NOTE: The Decomposition algorithm is using an aggregate formulation and Ryan-Foster

branching.

NOTE: The problem has a decomposable structure with 8 blocks. The largest block

covers 12.44% of the constraints in the problem.

NOTE: The decomposition subproblems cover 7560 (100.00%) variables and 4216 (99.50%)

constraints.

NOTE: The deterministic parallel mode is enabled.

NOTE: The Decomposition algorithm is using up to 4 threads.

Iter Best Master Best LP IP CPU Real

Bound Objective Integer Gap Gap Time Time

NOTE: Starting phase 1.

1 0.0000 20.0000 . 2.00e+01 . 0 0

20 0.0000 0.9286 . 9.29e-01 . 6 7

27 0.0000 0.0000 . 0.00% . 10 10

NOTE: Starting phase 2.

. 112.0000 801.0000 801.0000 615.18% 615.18% 10 10

. 112.0000 801.0000 801.0000 615.18% 615.18% 11 12

33 122.8333 798.1667 801.0000 549.80% 552.10% 19 19

39 214.2800 696.2000 801.0000 224.90% 273.81% 26 27

. 214.2800 690.0000 801.0000 222.01% 273.81% 26 27

40 214.2800 690.0000 801.0000 222.01% 273.81% 27 27

41 265.9412 683.3529 801.0000 156.96% 201.19% 30 30

42 379.6667 681.5333 801.0000 79.51% 110.97% 35 36

44 433.3590 660.4359 801.0000 52.40% 84.84% 41 42

. 433.3590 642.1667 683.9999 48.18% 57.84% 53 54

51 437.0526 635.7895 683.9999 45.47% 56.50% 57 58

53 472.1887 631.3585 683.9999 33.71% 44.86% 64 65

54 531.0833 627.3056 683.9999 18.12% 28.79% 70 71

. 531.0833 607.7500 614.0000 14.44% 15.61% 86 87

60 531.0833 607.7500 614.0000 14.44% 15.61% 88 89

62 573.7500 605.7500 614.0000 5.58% 7.02% 97 98

63 582.7500 604.7500 614.0000 3.78% 5.36% 104 105

64 582.7500 604.0000 604.0000 3.65% 3.65% 110 112

65 588.0000 604.0000 604.0000 2.72% 2.72% 122 123

66 595.8333 603.8333 604.0000 1.34% 1.37% 135 137

67 597.1667 603.8333 604.0000 1.12% 1.14% 148 150

68 597.1667 603.0000 603.0000 0.98% 0.98% 156 158

69 603.0000 603.0000 603.0000 0.00% 0.00% 171 173

Node Active Sols Best Best Gap CPU Real

Integer Bound Time Time

0 0 9 603.0000 603.0000 0.00% 171 173

NOTE: The Decomposition algorithm used 1 threads.

NOTE: The Decomposition algorithm time is 173.41 seconds.

NOTE: Optimal.

NOTE: Objective = 603.

NOTE: The data set WORK.NODE_DATA has 22 observations and 3 variables.

NOTE: The data set WORK.EDGE_DATA has 29 observations and 8 variables.

The following DATA step and call to PROC SGPLOT generate a plot of the optimal routing. The plot is displayed in Output 14.7.3.

data sganno(drop=i j);
   retain drawspace "datavalue" linethickness 1;
   set edge_data;
   function = 'line';
run;

proc sgplot data=node_data sganno=sganno;
   scatter x=x y=y / datalabel=i;
   xaxis display=none;
   yaxis display=none;
run;

Output 14.7.3: Optimal Routing