The Nonlinear Programming Solver
Example 7.2 Solving Unconstrained and Bound-Constrained Optimization Problems
Although the NLP techniques are suited for solving generally constrained nonlinear optimization problems, these techniques can also be used to solve unconstrained and bound-constrained problems efficiently. This example considers the relatively large nonlinear optimization problems
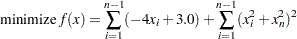 |
and
 |
with  . These problems are unconstrained and bound-constrained, respectively.
. These problems are unconstrained and bound-constrained, respectively.
For large-scale problems, the default memory limit might be too small, which can lead to out-of-memory status. To prevent this occurrence, it is recommended that you set a larger memory size. See the section Memory Limit for more information.
To solve the first problem, you can write the following statements:
proc optmodel;
number N=100000;
var x{1..N} init 1.0;
minimize f = sum {i in 1..N - 1} (-4 * x[i] + 3.0) +
sum {i in 1..N - 1} (x[i]^2 + x[N]^2)^2;
solve with nlp;
quit;
The problem and solution summaries are shown in Output 7.2.1.
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | f |
| Objective Type | Nonlinear |
| Number of Variables | 100000 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 0 |
| Free | 100000 |
| Fixed | 0 |
| Number of Constraints | 0 |
| Solution Summary | |
|---|---|
| Solver | NLP/INTERIORPOINT |
| Objective Function | f |
| Solution Status | Optimal |
| Objective Value | 0 |
| Iterations | 15 |
| Optimality Error | 6.560187E-13 |
| Infeasibility | 0 |
To solve the second problem, you can write the following statements (here the active-set method is specifically selected):
proc optmodel;
number N=100000;
var x{1..N} >= 1 <= 2;
minimize f = sum {i in 1..N - 1} cos(-0.5*x[i+1] - x[i]^2);
solve with nlp / tech=ActiveSet;
quit;
The problem and solution summaries are shown in Output 7.2.2.
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | f |
| Objective Type | Nonlinear |
| Number of Variables | 100000 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 100000 |
| Free | 0 |
| Fixed | 0 |
| Number of Constraints | 0 |
| Solution Summary | |
|---|---|
| Solver | NLP/ACTIVESET |
| Objective Function | f |
| Solution Status | Optimal |
| Objective Value | -99999 |
| Iterations | 4 |
| Optimality Error | 1.57688E-10 |
| Infeasibility | 0 |
