The Nonlinear Programming Solver
| Basic Definitions and Notation |
The gradient of a function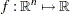 
is the vector of all the first partial derivatives of 
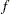and is denoted by
 |
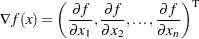where the superscript T denotes the transpose of a vector.
The Hessian matrix of 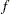, denoted by 
, or simply by 
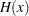, is an 
symmetric matrix whose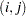 
element is the second partial derivative of 
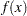with respect to 
and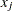 
. That is, 
.
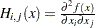Consider the vector function, 
, whose first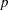 
elements are the equality constraint functions 
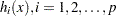, and whose last 
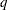elements are the inequality constraint functions 
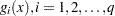. That is,
 |
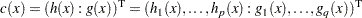The 
matrix whose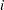 
th column is the gradient of the 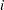th element of 
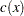is called the Jacobian matrix of 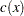(or simply the Jacobian of the NLP problem) and is denoted by 
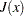. You can also use 
to denote the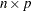 
Jacobian matrix of the equality constraints and use 
to denote the 
Jacobian matrix of the inequality constraints. It is easy to see that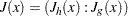 
.