The Nonlinear Programming Solver: Solving Highly Nonlinear Optimization Problems

Example 7.1 Solving Highly Nonlinear Optimization Problems

This example demonstrates the use of the NLP solver to solve the following highly nonlinear optimization problem, which appears in Hock and Schittkowski (1981):

$\text{[math]}$

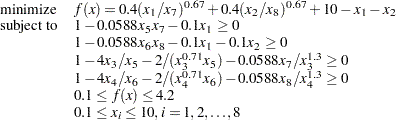The initial point used is 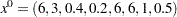$\text{[math]}$ . You can call the NLP solver within PROC OPTMODEL to solve the problem by writing the following SAS statements:

proc optmodel;
   var x{1..8} >= 0.1 <= 10;
   
   min f = 0.4*(x[1]/x[7])^0.67 + 0.4*(x[2]/x[8])^0.67 + 10 - x[1] - x[2];

   con c1: 1 - 0.0588*x[5]*x[7] - 0.1*x[1] >= 0;
   con c2: 1 - 0.0588*x[6]*x[8] - 0.1*x[1] - 0.1*x[2] >= 0;
   con c3: 1 - 4*x[3]/x[5] - 2/(x[3]^0.71*x[5]) - 0.0588*x[7]/x[3]^1.3 >= 0;
   con c4: 1 - 4*x[4]/x[6] - 2/(x[4]^0.71*x[6]) - 0.0588*x[8]/x[4]^1.3 >= 0;
   con c5: 0.1 <= f <= 4.2;

   /* starting point */
   x[1] = 6;
   x[2] = 3;
   x[3] = 0.4;
   x[4] = 0.2;
   x[5] = 6;
   x[6] = 6;
   x[7] = 1;
   x[8] = 0.5;
   
   solve with nlp / tech=ActiveSet;
   print x;
 quit;

The summaries and the solution are shown in Output 7.1.1.

Output 7.1.1 Summaries and the Optimal Solution

The OPTMODEL Procedure

Problem Summary
Objective Sense	Minimization
Objective Function	f
Objective Type	Nonlinear

Number of Variables	8
Bounded Above	0
Bounded Below	0
Bounded Below and Above	8
Free	0
Fixed	0

Number of Constraints	5
Linear LE (<=)	0
Linear EQ (=)	0
Linear GE (>=)	0
Linear Range	0
Nonlinear LE (<=)	0
Nonlinear EQ (=)	0
Nonlinear GE (>=)	4
Nonlinear Range	1

Solution Summary
Solver	NLP/ACTIVESET
Objective Function	f
Solution Status	Optimal
Objective Value	3.9511649783
Iterations	18

Optimality Error	8.3192274E-8
Infeasibility	1.4434128E-8

[1]	x
1	6.46512
2	2.23270
3	0.66740
4	0.59577
5	5.93267
6	5.52724
7	1.01332
8	0.40067