| The NLP Procedure |
Example 4.8: Chemical Equilibrium
The following example is used in many test libraries for nonlinear programming and was taken originally from Bracken and McCormick (1968).
The problem is to determine the composition of a mixture of various chemicals satisfying its chemical equilibrium state. The second law of thermodynamics implies that a mixture of chemicals satisfies its chemical equilibrium state (at a constant temperature and pressure) when the free energy of the mixture is reduced to a minimum. Therefore the composition of the chemicals satisfying its chemical equilibrium state can be found by minimizing the function of the free energy of the mixture.
Notation:
| number of chemical elements in the mixture | |
| number of compounds in the mixture | |
| number of moles for compound | |
| total number of moles in the mixture | |
| number of atoms of element | |
| atomic weight of element |
Constraints for the Mixture:
- The number of moles must be positive:
- There are
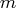 mass balance relationships,
mass balance relationships,
Objective Function: Total Free Energy of Mixture
where ![]() is the model standard free
energy function for the
is the model standard free
energy function for the ![]() th compound (found
in tables) and
th compound (found
in tables) and ![]() is the total pressure in atmospheres.
is the total pressure in atmospheres.
Minimization Problem:
Determine the parameters ![]() that minimize the
objective function
that minimize the
objective function ![]() subject to the nonnegativity
and linear balance constraints.
subject to the nonnegativity
and linear balance constraints.
Numeric Example:
Determine the equilibrium composition of compound
![]() at temperature
at temperature
![]() and pressure
and pressure ![]() .
.
| Compound | ||||||
| 1 | -10.021 | -6.089 | 1 | |||
| 2 | -21.096 | -17.164 | 2 | |||
| 3 | -37.986 | -34.054 | 2 | 1 | ||
| 4 | -9.846 | -5.914 | 1 | |||
| 5 | -28.653 | -24.721 | 2 | |||
| 6 | -18.918 | -14.986 | 1 | 1 | ||
| 7 | -28.032 | -24.100 | 1 | 1 | ||
| 8 | -14.640 | -10.708 | 1 | |||
| 9 | -30.594 | -26.662 | 2 | |||
| 10 | -26.111 | -22.179 | 1 | 1 | ||
Example Specification:
proc nlp tech=tr pall;
array c[10] -6.089 -17.164 -34.054 -5.914 -24.721
-14.986 -24.100 -10.708 -26.662 -22.179;
array x[10] x1-x10;
min y;
parms x1-x10 = .1;
bounds 1.e-6 <= x1-x10;
lincon 2. = x1 + 2. * x2 + 2. * x3 + x6 + x10,
1. = x4 + 2. * x5 + x6 + x7,
1. = x3 + x7 + x8 + 2. * x9 + x10;
s = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10;
y = 0.;
do j = 1 to 10;
y = y + x[j] * (c[j] + log(x[j] / s));
end;
run;
Displayed Output:
The iteration history given in Output 4.8.1 does not show any problems.
Output 4.8.1: Iteration HistoryOutput 4.8.2 lists the optimal parameters with the gradient.
Output 4.8.2: Optimization ResultsPROC NLP: Nonlinear Minimization
Value of Objective Function = -47.76109086
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
The three equality constraints are satisfied at the solution, as shown in Output 4.8.3.
Output 4.8.3: Linear Constraints at SolutionPROC NLP: Nonlinear Minimization
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The Lagrange multipliers are given in Output 4.8.4.
Output 4.8.4: Lagrange MultipliersThe elements of the projected gradient must be small to satisfy a necessary first-order optimality condition. The projected gradient is given in Output 4.8.5.
Output 4.8.5: Projected GradientThe projected Hessian matrix shown in Output 4.8.6 is positive definite, satisfying the second-order optimality condition.
Output 4.8.6: Projected Hessian MatrixPROC NLP: Nonlinear Minimization
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The following PROC NLP call uses a specified analytical gradient and the Hessian matrix is computed by finite-difference approximations based on the analytic gradient:
proc nlp tech=tr fdhessian all;
array c[10] -6.089 -17.164 -34.054 -5.914 -24.721
-14.986 -24.100 -10.708 -26.662 -22.179;
array x[10] x1-x10;
array g[10] g1-g10;
min y;
parms x1-x10 = .1;
bounds 1.e-6 <= x1-x10;
lincon 2. = x1 + 2. * x2 + 2. * x3 + x6 + x10,
1. = x4 + 2. * x5 + x6 + x7,
1. = x3 + x7 + x8 + 2. * x9 + x10;
s = x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10;
y = 0.;
do j = 1 to 10;
y = y + x[j] * (c[j] + log(x[j] / s));
g[j] = c[j] + log(x[j] / s);
end;
run;
The results are almost identical to those of the previous run.
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
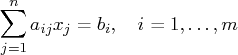
![f(x) = \sum_{j=1}^n x_j [c_j + \ln ( \frac{x_j}s ) ]](images/nlp_nlpeq529.gif)