PROC NLP: Example 4.7: Simple Pooling Problem :: SAS/OR(R) 9.2 User's Guide: Mathematical Programming

The NLP Procedure

Example 4.7: Simple Pooling Problem

The following optimization problem is discussed in Haverly (1978) and in Liebman et al. (1986, pp. 127--128). Two liquid chemicals, and , are produced by the pooling and blending of three input liquid chemicals, , , and . You know the sulfur impurity amounts of the input chemicals, and you have to respect upper limits of the sulfur impurity amounts of the output chemicals. The sulfur concentrations and the prices of the input and output chemicals are:

Chemical 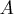: Concentration = 3%, Price= $6
Chemical 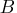: Concentration = 1%, Price= $16
Chemical 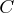: Concentration = 2%, Price= $10
Chemical 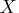: Concentration 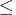$\leq$ 2.5%, Price= $9
Chemical 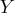: Concentration 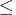$\leq$ 1.5%, Price= $15

The problem is complicated by the fact that the two input chemicals

and

are available only as a mixture (they are either shipped together or stored together). Because the amounts of

and

are unknown, the sulfur concentration of the mixture is also unknown.

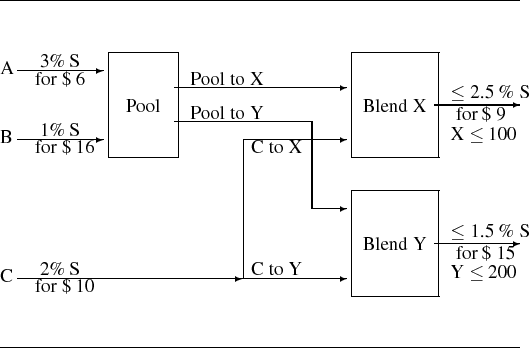
$\begin{picture} (300.,200.) \put(0,200){\line(1,0){300}} \put(0,38)c \put(0,1... ...vector(1,0){60}} \put(145,112){c to x} \put(0,0){\line(1,0){300}}\end{picture}$

You know customers will buy no more than 100 units of X and 200 units of Y. The problem is determining how to operate the pooling and blending of the chemicals to maximize the profit. The objective function for the profit is

${profit} & = & {cost}(x) x {amount}(x) + {cost}(y) x {amount}(y) \ & - & {cost}(a) x {amount}(a) - {cost}(b) x {amount}(b) - {cost}(c) x {amount}(c)$

There are three groups of constraints:

The first group of constraint functions is the mass balance restrictions illustrated by the graph. These are four linear equality constraints:
- ${amount}(a) + {amount}(b) = {pool\_to\_x} + {pool\_to\_y}$
- ${pool\_to\_x} + {c\_to\_x} = {amount}(x)$
- ${pool\_to\_y} + {c\_to\_y} = {amount}(y)$
- ${amount}(c) = {c\_to\_x} + {c\_to\_y}$
You introduce a new variable, 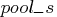, that represents the sulfur concentration of the pool. Using 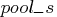and the sulfur concentration of 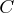(2%), you obtain two nonlinear inequality constraints for the sulfur concentrations of 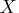and 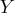, one linear equality constraint for the sulfur balance, and lower and upper boundary restrictions for :
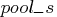- ${pool\_s} x {pool\_to\_x} + 2 \, {c\_to\_x} \leq 2.5 \, {amount}(x)$
- ${pool\_s} x {pool\_to\_y} + 2 \, {c\_to\_y} \leq 1.5 \, {amount}(y)$
- $3 \, {amount}(a) + 1 \, {amount}(b) = {pool\_s} x ({amount}(a) + {amount}(b))$
- $1 \leq {pool\_s} \leq 3$
The last group assembles the remaining boundary constraints. First, you do not want to produce more than you can sell; and finally, all variables must be nonnegative:
- ${amount}(x) \leq 100, {amount}(y) \leq 200$
- ${amount}(a), {amount}(b), {amount}(c), {amount}(x), {amount}(y) \geq 0$
- ${pool\_to\_x}, {pool\_to\_y}, {c\_to\_x}, {c\_to\_y} \geq 0$

There exist several local optima to this problem that can be found by specifying different starting points. Using the starting point with all variables equal to 1 (specified with a PARMS statement), PROC NLP finds a solution with :

  
    proc nlp all; 
       parms amountx amounty amounta amountb amountc 
             pooltox pooltoy ctox ctoy pools = 1; 
       bounds 0 <= amountx amounty amounta amountb amountc, 
                   amountx <= 100, 
                   amounty <= 200, 
              0 <= pooltox pooltoy ctox ctoy, 
              1 <= pools <= 3; 
       lincon amounta + amountb = pooltox + pooltoy, 
              pooltox + ctox = amountx, 
              pooltoy + ctoy = amounty, 
              ctox + ctoy    = amountc; 
       nlincon nlc1-nlc2 >= 0., 
               nlc3 = 0.; 
       max f; 
       costa = 6; costb = 16; costc = 10; 
       costx = 9; costy = 15; 
       f = costx * amountx + costy * amounty 
           - costa * amounta - costb * amountb - costc * amountc; 
       nlc1 = 2.5 * amountx - pools * pooltox - 2. * ctox; 
       nlc2 = 1.5 * amounty - pools * pooltoy - 2. * ctoy; 
       nlc3 = 3 * amounta + amountb - pools * (amounta + amountb); 
    run;

The specified starting point was not feasible with respect to the linear equality constraints; therefore, a starting point is generated that satisfies linear and boundary constraints. Output 4.7.1 gives the starting parameter estimates.

Output 4.7.1: Starting Estimates

PROC NLP: Nonlinear Maximization

Optimization Start
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function	Gradient Lagrange Function	Lower Bound Constraint	Upper Bound Constraint
1	amountx	1.363636	9.000000	-0.843698	0	100.000000
2	amounty	1.363636	15.000000	-0.111882	0	200.000000
3	amounta	0.818182	-6.000000	-0.430733	0	.
4	amountb	0.818182	-16.000000	-0.542615	0	.
5	amountc	1.090909	-10.000000	0.017768	0	.
6	pooltox	0.818182	0	-0.669628	0	.
7	pooltoy	0.818182	0	-0.303720	0	.
8	ctox	0.545455	0	-0.174070	0	.
9	ctoy	0.545455	0	0.191838	0	.
10	pools	2.000000	0	0.068372	1.000000	3.000000

Value of Objective Function = 3.8181818182

Value of Lagrange Function = -2.866739915

The starting point satisfies the four equality constraints, as shown in Output 4.7.2. The nonlinear constraints are given in Output 4.7.3.

Output 4.7.2: Linear Constraints

Linear Constraints
1	2.2204E-16	:	ACT	==	+	1.0000	*	amounta	+	1.0000	*	amountb	-	1.0000	*	pooltox	-	1.0000	*	pooltoy
2	0	:	ACT	==	-	1.0000	*	amountx	+	1.0000	*	pooltox	+	1.0000	*	ctox
3	-1.11E-16	:	ACT	==	-	1.0000	*	amounty	+	1.0000	*	pooltoy	+	1.0000	*	ctoy
4	-1.11E-16	:	ACT	==	-	1.0000	*	amountc	+	1.0000	*	ctox	+	1.0000	*	ctoy

Output 4.7.3: Nonlinear Constraints

Values of Nonlinear Constraints
Constraint				Value	Residual	Lagrange Multiplier
[	5	]	nlc3	0	0	4.9441	Active NLEC
[	6	]	nlc1_G	0.6818	0.6818	.
[	7	]	nlc2_G	-0.6818	-0.6818	-9.8046	Violat. NLIC

Output 4.7.4 shows the settings of some important PROC NLP options.

Output 4.7.4: Options

PROC NLP: Nonlinear Maximization

Minimum Iterations	0
Maximum Iterations	200
Maximum Function Calls	500
Iterations Reducing Constraint Violation	20
ABSGCONV Gradient Criterion	0.00001
GCONV Gradient Criterion	1E-8
ABSFCONV Function Criterion	0
FCONV Function Criterion	2.220446E-16
FCONV2 Function Criterion	1E-6
FSIZE Parameter	0
ABSXCONV Parameter Change Criterion	0
XCONV Parameter Change Criterion	0
XSIZE Parameter	0
ABSCONV Function Criterion	1.340781E154
Line Search Method	2
Starting Alpha for Line Search	1
Line Search Precision LSPRECISION	0.4
DAMPSTEP Parameter for Line Search	.
FD Derivatives: Accurate Digits in Obj.F	15.653559775
FD Derivatives: Accurate Digits in NLCon	15.653559775
Singularity Tolerance (SINGULAR)	1E-8
Constraint Precision (LCEPS)	1E-8
Linearly Dependent Constraints (LCSING)	1E-8
Releasing Active Constraints (LCDEACT)	.

The iteration history, given in Output 4.7.5, does not show any problems.

Output 4.7.5: Iteration History

PROC NLP: Nonlinear Maximization

Dual Quasi-Newton Optimization

Modified VMCWD Algorithm of Powell (1978, 1982)

Dual Broyden - Fletcher - Goldfarb - Shanno Update (DBFGS)

Lagrange Multiplier Update of Powell(1982)

Iteration		Function Calls	Objective Function	Maximum Constraint Violation	Predicted Function Reduction	Step Size	Maximum Gradient Element of the Lagrange Function
1		19	-1.42400	0.00962	6.9131	1.000	0.783
2	'	20	2.77026	0.0166	5.3770	1.000	2.629
3		21	7.08706	0.1409	7.1965	1.000	9.452
4	'	22	11.41264	0.0583	15.5769	1.000	23.390
5	'	23	24.84613	1.78E-15	496.1	1.000	147.6
6		24	378.22825	147.4	3316.7	1.000	840.4
7	'	25	307.56810	50.9339	607.9	1.000	27.143
8	'	26	347.24468	1.8329	21.9883	1.000	28.482
9	'	27	349.49255	0.00915	7.1833	1.000	28.289
10	'	28	356.58341	0.1083	50.2566	1.000	27.479
11	'	29	388.70731	2.4280	24.7996	1.000	21.114
12	'	30	389.30118	0.0157	10.0475	1.000	18.647
13	'	31	399.19240	0.7997	11.1862	1.000	0.416
14	'	32	400.00000	0.0128	0.1533	1.000	0.00087
15	'	33	400.00000	7.38E-11	2.43E-10	1.000	365E-12

Optimization Results
Iterations	15	Function Calls	34
Gradient Calls	18	Active Constraints	10
Objective Function	400	Maximum Constraint Violation	7.381118E-11
Maximum Projected Gradient	0	Value Lagrange Function	-400
Maximum Gradient of the Lagran Func	4.973799E-14	Slope of Search Direction	-2.43338E-10

FCONV2 convergence criterion satisfied.

The optimal solution in Output 4.7.6 shows that to obtain the maximum profit of $400, you need only to produce the maximum 200 units of blending and no units of blending .

Output 4.7.6: Optimization Solution

PROC NLP: Nonlinear Maximization

Optimization Results
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function	Gradient Lagrange Function	Active Bound Constraint
1	amountx	-1.40478E-11	9.000000	0	Lower BC
2	amounty	200.000000	15.000000	-8.88178E-16	Upper BC
3	amounta	5.763446E-16	-6.000000	0	Lower BC
4	amountb	100.000000	-16.000000	1.065814E-14
5	amountc	100.000000	-10.000000	-1.77636E-15
6	pooltox	7.024487E-12	0	0	Lower BC
7	pooltoy	100.000000	0	1.776357E-15
8	ctox	-2.10722E-11	0	1.776357E-15	Lower BC	LinDep
9	ctoy	100.000000	0	5.329071E-15
10	pools	1.000000	0	4.973799E-14	Lower BC	LinDep

Value of Objective Function = 400

Value of Lagrange Function = 400

The constraints are satisfied at the solution, as shown in Output 4.7.7

Output 4.7.7: Linear and Nonlinear Constraints at the Solution

Linear Constraints Evaluated at Solution
1	ACT	0	=	+	1.0000	*	amounta	+	1.0000	*	amountb	-	1.0000	*	pooltox	-	1.0000	*	pooltoy
2	ACT	6.582E-17	=	-	1.0000	*	amountx	+	1.0000	*	pooltox	+	1.0000	*	ctox
3	ACT	0	=	-	1.0000	*	amounty	+	1.0000	*	pooltoy	+	1.0000	*	ctoy
4	ACT	0	=	-	1.0000	*	amountc	+	1.0000	*	ctox	+	1.0000	*	ctoy

Values of Nonlinear Constraints
Constraint				Value	Residual	Lagrange Multiplier
[	5	]	nlc3	1.15E-15	1.15E-15	6.0000	Active NLEC
[	6	]	nlc1_G	4.57E-16	4.57E-16	.	Active NLIC	LinDep
[	7	]	nlc2_G	0	0	-6.0000	Active NLIC

Linearly Dependent Active Boundary Constraints
Parameter	N	Kind
ctox	8	Lower BC
pools	10	Lower BC

Linearly Dependent Gradients of Active Nonlinear Constraints
Parameter	N
nlc3	6

The same problem can be specified in many different ways. For example, the following specification uses an INEST= data set containing the values of the starting point and of the constants COST, COSTB, COSTC, COSTX, COSTY, CA, CB, CC, and CD:

  
    data init1(type=est); 
       input _type_ $ amountx amounty amounta amountb 
             amountc pooltox pooltoy ctox ctoy pools 
             _rhs_ costa costb costc costx costy 
             ca cb cc cd; 
       datalines; 
    parms  1 1 1 1 1 1 1 1 1 1 
           . 6 16 10 9 15  2.5 1.5 2. 3. 
    ;

  
    proc nlp inest=init1 all; 
       parms amountx amounty amounta amountb amountc 
             pooltox pooltoy ctox ctoy pools; 
       bounds 0 <= amountx amounty amounta amountb amountc, 
                   amountx <= 100, 
                   amounty <= 200, 
              0 <= pooltox pooltoy ctox ctoy, 
              1 <= pools <= 3; 
       lincon amounta + amountb = pooltox + pooltoy, 
              pooltox + ctox = amountx, 
              pooltoy + ctoy = amounty, 
              ctox + ctoy    = amountc; 
       nlincon nlc1-nlc2 >= 0., 
               nlc3 = 0.; 
       max f; 
       f = costx * amountx + costy * amounty 
           - costa * amounta - costb * amountb - costc * amountc; 
       nlc1 = ca * amountx - pools * pooltox - cc * ctox; 
       nlc2 = cb * amounty - pools * pooltoy - cc * ctoy; 
       nlc3 = cd * amounta + amountb - pools * (amounta + amountb); 
    run;

The third specification uses an INEST= data set containing the boundary and linear constraints in addition to the values of the starting point and of the constants. This specification also writes the model specification into an OUTMOD= data set:

  
    data init2(type=est); 
       input _type_ $ amountx amounty amounta amountb amountc 
                     pooltox pooltoy ctox ctoy pools 
                     _rhs_ costa costb costc costx costy; 
       datalines; 
    parms      1   1  1  1  1    1   1   1  1  1 
               .   6 16 10  9   15 2.5 1.5  2  3 
    lowerbd    0   0  0  0  0    0   0   0  0  1 
               .   .  .  .  .    .   .   .  .  . 
    upperbd  100 200  .  .  .    .   .   .  .  3 
               .   .  .  .  .    .   .   .  .  . 
    eq         .   .  1  1  .   -1  -1   .  .  . 
               0   .  .  .  .    .   .   .  .  . 
    eq         1   .  .  .  .   -1   .  -1  .  . 
               0   .  .  .  .    .   .   .  .  . 
    eq         .   1  .  .  .    .  -1   . -1  . 
               0   .  .  .  .    .   .   .  .  . 
    eq         .   .  .  .  1    .   .  -1 -1  . 
               0   .  .  .  .    .   .   .  .  . 
    ;

  
    proc nlp inest=init2 outmod=model all; 
       parms amountx amounty amounta amountb amountc 
             pooltox pooltoy ctox ctoy pools; 
       nlincon nlc1-nlc2 >= 0., 
               nlc3 = 0.; 
       max f; 
       f = costx * amountx + costy * amounty 
           - costa * amounta - costb * amountb - costc * amountc; 
       nlc1 = 2.5 * amountx - pools * pooltox - 2. * ctox; 
       nlc2 = 1.5 * amounty - pools * pooltoy - 2. * ctoy; 
       nlc3 = 3 * amounta + amountb - pools * (amounta + amountb); 
    run;

The fourth specification not only reads the INEST=INIT2 data set, it also uses the model specification from the MODEL data set that was generated in the last specification. The PROC NLP call now contains only the defining variable statements:

  
    proc nlp inest=init2 model=model all; 
       parms amountx amounty amounta amountb amountc 
             pooltox pooltoy ctox ctoy pools; 
       nlincon nlc1-nlc2 >= 0., 
               nlc3 = 0.; 
       max f; 
    run;

All four specifications start with the same starting point of all variables equal to 1 and generate the same results. However, there exist several local optima to this problem, as is pointed out in Liebman et al. (1986, p. 130).

  
    proc nlp inest=init2 model=model all; 
       parms amountx amounty amounta amountb amountc 
             pooltox pooltoy ctox ctoy = 0, 
             pools = 2; 
       nlincon nlc1-nlc2 >= 0., 
               nlc3 = 0.; 
       max f; 
    run;

This starting point with all variables equal to 0 is accepted as a local solution with , which minimizes rather than maximizes the profit.

Top of Page