The RANDMULTINOMIAL function is part of the IMLMLIB library. The RANDMULTINOMIAL function generates a random sample from a multinomial distribution, which is a multivariate generalization of the binomial distribution.
The input parameters are as follows:
- N
-
is the number of observations to sample.
- NumTrials
-
is the number of trials.
![$NumTrials[j] \geq 0$](images/imlug_langref1212.png) , for
, for 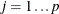 .
.
- Prob
-
is a
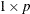 vector of probabilities with
vector of probabilities with ![$0 < \mi {Prob}[j] \leq 1$](images/imlug_langref1215.png) and
and ![$\Sigma _{j=1}^ p \mbox{Prob}[j] = 1$](images/imlug_langref1216.png) .
.
For each trial, ![]() is the probability of event
is the probability of event ![]() , where the
, where the ![]() are mutually exclusive and
are mutually exclusive and ![]() .
.
The RANDMULTINOMIAL function returns an ![]() matrix that contains
matrix that contains ![]() observations of
observations of ![]() random draws from the multinomial distribution. Each row of the resulting matrix is an integer vector
random draws from the multinomial distribution. Each row of the resulting matrix is an integer vector ![]() with
with ![]() . That is, for each row,
. That is, for each row, ![]() indicates how many times event
indicates how many times event ![]() occurred in
occurred in ![]() trials.
trials.
If ![]() follows a multinomial distribution with
follows a multinomial distribution with ![]() trials and probabilities
trials and probabilities ![]() , then
, then
-
the probability density function for
 is
is
![\[ f(x; n, \rho )= \frac{n!}{ \prod _{i=1}^ p {x_ i!}} \prod _{i=1}^ p {{\rho _ i}^{x_ i}} \]](images/imlug_langref1223.png)
-
the expected value of
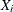 is
is 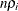 .
.
-
the variance of
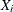 is
is 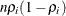 .
.
-
the covariance of
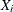 with
with 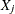 is
is 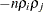 .
.
-
if
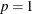 then
then 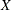 is constant.
is constant.
-
if
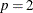 then
then 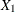 is Binomial
is Binomial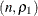 and
and 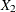 is Binomial
is Binomial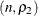 .
.
The following example generates 1,000 samples from a multinomial distribution with three mutually exclusive events. For each
sample, 10 events are generated. Each row of the returned matrix x represents the number of times each event is observed. The example also computes the sample mean and covariance and compares
them with the expected values.
call randseed(1);
prob = {0.3,0.6,0.1};
NumTrials = 10;
N = 1000;
x = RandMultinomial(N,NumTrials,prob);
/* population mean and covariance */
Mean = NumTrials * prob`;
Cov = -NumTrials*prob*prob`;
/* replace diagonal elements of Cov with Variance */
Variance = NumTrials*prob#(1-prob);
do i = 1 to nrow(prob);
Cov[i,i] = Variance[i];
end;
SampleMean = mean(x);
SampleCov = cov(x);
print SampleMean Mean, SampleCov Cov;
Figure 24.300: Estimated Mean and Covariance Matrix
| SampleMean | Mean | ||||
|---|---|---|---|---|---|
| 2.891 | 6.059 | 1.05 | 3 | 6 | 1 |
| SampleCov | Cov | ||||
|---|---|---|---|---|---|
| 2.0051241 | -1.69126 | -0.313864 | 2.1 | -1.8 | -0.3 |
| -1.69126 | 2.3198388 | -0.628579 | -1.8 | 2.4 | -0.6 |
| -0.313864 | -0.628579 | 0.9424424 | -0.3 | -0.6 | 0.9 |
For further details about sampling from the multinomial distribution, see Gentle (2003), or Fishman (1996).