| FARMALIK Call |
The FARMALIK subroutine evaluates the log-likelihood function of an ARFIMA(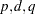 ) model for a given time series.
) model for a given time series.
The input arguments to the FARMALIK subroutine are as follows:
- series
specifies a time series (assuming mean zero).
- d
specifies a fractional differencing order. This argument is required; the value of
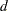 should be in the open interval
should be in the open interval 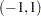 excluding zero.
excluding zero. - phi
specifies an
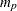 -dimensional vector that contains the autoregressive coefficients, where
-dimensional vector that contains the autoregressive coefficients, where 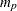 is the number of the elements in the subset of the AR order. The default is zero.
is the number of the elements in the subset of the AR order. The default is zero. - theta
specifies an
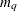 -dimensional vector that contains the moving average coefficients, where
-dimensional vector that contains the moving average coefficients, where 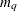 is the number of the elements in the subset of the MA order. The default is zero.
is the number of the elements in the subset of the MA order. The default is zero. - sigma
specifies a variance of the innovation series. The default is one.
- p
specifies the subset of the AR order. See the FARMACOV subroutine for additional details.
- q
specifies the subset of the MA order. See the FARMACOV subroutine for additional details.
- opt
-
specifies the method of computing the log-likelihood function. The following are valid values:
- 0
requests the conditional sum of squares function. This is the default.
- 1
requests the exact log-likelihood function. This option requires that the time series be stationary and invertible.
The FARMALIK subroutine returns the following value:
- lnl
is a three-dimensional vector. If opt
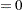 is specified, the conditional sum of squares function is evaluated and the result returns in lnl[1]. Otherwise, lnl[1] contains the log-likelihood function of the model; lnl[2] contains the sum of the log determinant of the innovation variance; and lnl[3] contains the weighted sum of squares of residuals. The log-likelihood function is computed as
is specified, the conditional sum of squares function is evaluated and the result returns in lnl[1]. Otherwise, lnl[1] contains the log-likelihood function of the model; lnl[2] contains the sum of the log determinant of the innovation variance; and lnl[3] contains the weighted sum of squares of residuals. The log-likelihood function is computed as  (lnl[2]+lnl[3]).
(lnl[2]+lnl[3]).
As an example, consider the following ARFIMA( ) model:
) model:
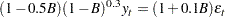 |
In this model, 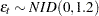 . The following statements compute the log-likelihood function of this model:
. The following statements compute the log-likelihood function of this model:
d = 0.3; phi = 0.5; theta = -0.1; sigma = 1.2; call farmasim(yt, d, phi, theta, sigma) seed=1234; call farmalik(lnl, yt, d, phi, theta, sigma); print (lnl[1])[label="Conditional Sum of Squares"];
| Conditional Sum of Squares |
|---|
| -16.67587 |
The FARMALIK subroutine computes a log-likelihood function of the ARFIMA(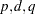 ) model. The exact log-likelihood function was proposed by Sowell (1992); the conditional sum of squares function was proposed by Chung (1996).
) model. The exact log-likelihood function was proposed by Sowell (1992); the conditional sum of squares function was proposed by Chung (1996).
The exact log-likelihood function only considers a stationary and invertible ARFIMA(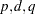 ) process with
) process with 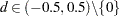 represented as
represented as
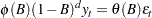 |
where 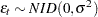 .
.
Let 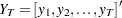 and the log-likelihood function is as follows without a constant term:
and the log-likelihood function is as follows without a constant term:
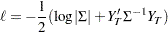 |
where 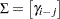 for
for 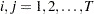 .
.
The conditional sum of squares function does not require the normality assumption. The initial observations 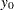 ,
, 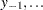 and
and 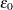 ,
, 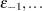 are set to zero.
are set to zero.
Let 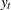 be an ARFIMA(
be an ARFIMA(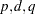 ) process represented as
) process represented as
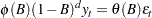 |
Then the conditional sum of squares function is
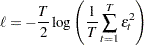 |