Robust Regression Examples

Combining Robust Residual and Robust Distance

This section is based entirely on Rousseeuw and Van Zomeren (1990). Observations , which are far away from most of the other observations, are called leverage points. One classical method inspects the Mahalanobis distances to find outliers :

$md_i = \sqrt{(x_i - \mu) c^{-1}(x_i - \mu)^t}$

where

is the classical sample covariance matrix.

Note that the MVE subroutine prints the classical Mahalanobis distances together with the robust distances . In classical linear regression, the diagonal elements $h_{ii}$ of the hat matrix

$h = x(x^t{x})^{-1}x^t$

are used to identify leverage points. Rousseeuw and Van Zomeren (1990) report the following monotone relationship between the $h_{ii}$ and

$h_{ii} = \frac{(md_i)^2}{n-1} + \frac{1}n$

They point out that neither the

nor the $h_{ii}$ are entirely safe for detecting leverage points reliably. Multiple outliers do not necessarily have large

values because of the masking effect.

The definition of a leverage point is, therefore, based entirely on the outlyingness of and is not related to the response value . By including the value in the definition, Rousseeuw and Van Zomeren (1990) distinguish between the following:

Good leverage points are poi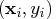nts that are close to the regression plane; that is, good leverage points improve the precision of the regression coefficients.
Bad leverage points are poi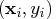nts that are far from the regression plane; that is, bad leverage points reduce the precision of the regression coefficients.

Rousseeuw and Van Zomeren (1990) propose to plot the standardized residuals of robust regression (LMS or LTS) versus the robust distances obtained from MVE. Two horizontal lines corresponding to residual values of and -2.5 are useful to distinguish between small and large residuals, and one vertical line corresponding to the $\sqrt{\chi^2_{n,.975}}$ is used to distinguish between small and large distances.

Example 9.6: Hawkins-Bradu-Kass Data

Example 9.7: Stackloss Data

Top of Page