| Language Reference |
RZLIND Call
computes rank deficient linear least squares solutions, complete orthogonal factorization, and Moore-Penrose inverses
- CALL RZLIND( lindep, rup, bup,
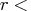 , sing<,
b>);
, sing<,
b>);
The RZLIND subroutine returns the following values:
- lindep
- is a
scalar giving the number of linear
dependencies that are recognized in
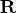 (number
of zeroed rows in rup[n,n]).
(number
of zeroed rows in rup[n,n]).
- rup
- is the
updated
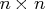 upper triangular
matrix
upper triangular
matrix 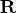 containing zero rows corresponding to
zero recognized diagonal elements in the original
containing zero rows corresponding to
zero recognized diagonal elements in the original 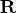 .
.
- bup
- is the
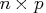 matrix
matrix 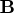 of right-hand
sides that is updated simultaneously with
of right-hand
sides that is updated simultaneously with 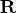 .
If
.
If 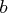 is not specified, bup is not accessible.
is not specified, bup is not accessible.
The inputs to the RZLIND subroutine are as follows:
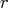
- specifies the
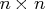 upper triangular matrix
upper triangular matrix 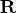 .
Only the upper triangle of
.
Only the upper triangle of 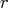 is used; the lower
triangle can contain any information.
is used; the lower
triangle can contain any information.
- sing
- is an
optional scalar specifying a relative
singularity criterion for the diagonal elements of
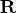 .
The diagonal element
.
The diagonal element 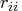 is considered zero if
is considered zero if
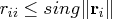 ,
where
,
where 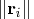 is the Euclidean
norm of column
is the Euclidean
norm of column 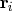 of
of 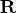 . If the value provided
for sing is not positive, the default value
sing
. If the value provided
for sing is not positive, the default value
sing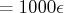 is used, where
is used, where 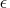 is
the relative machine precision.
is
the relative machine precision.
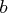
- specifies the
optional
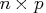 matrix
matrix 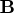 of
right-hand sides that have to be updated or downdated
simultaneously with
of
right-hand sides that have to be updated or downdated
simultaneously with 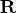 .
.
The singularity test used in the RZLIND subroutine is a relative test using the Euclidean norms of the columns
Consider the following possible application of the RZLIND subroutine. Assume that you want to compute the upper triangular Cholesky factor
In the following example,
a = {1 1 0 0 1 0 0,
1 1 0 0 1 0 0,
1 1 0 0 0 1 0,
1 1 0 0 0 0 1,
1 0 1 0 1 0 0,
1 0 1 0 0 1 0,
1 0 1 0 0 1 0,
1 0 1 0 0 0 1,
1 0 0 1 1 0 0,
1 0 0 1 0 1 0,
1 0 0 1 0 0 1,
1 0 0 1 0 0 1};
a = a || uniform(j(12,1,1));
aa = a` * a;
m = nrow(a); n = ncol(a);
Applying the ROOT function to the coefficient
matrix
r1 = root(aa);
ss1 = ssq(aa - r1` * r1);
print ss1 r1 [format=best6.];
Applying the QR subroutine with column pivoting on the original matrix
ord = j(n,1,0);
call qr(q,r2,pivqr,lindqr,a,ord);
ss2 = ssq(aa[pivqr,pivqr] - r2` * r2);
print ss2 r2 [format=best6.];
Using the RUPDT subroutine for stepwise updating of
r3 = shape(0,n,n);
call rupdt(rup,bup,sup,r3,a);
r3 = rup;
ss3 = ssq(aa - r3` * r3);
print ss3 r3 [format=best6.];
The result
call rzlind(lind,r4,bup,r3);
ss4 = ssq(aa - r4` * r4);
print ss4 r4 [format=best6.];
Consider the rank-deficient linear least squares problem:
b = uniform(j(12,1,1));
ab = a` * b;
print b a [format=best6.];
Each entry in the following list solves the rank-deficient linear least squares problem. Note that while each method minimizes the residual sum of squares, not all of the given solutions are of minimum Euclidean length.
- Use the singular value decomposition of
 , given by
, given by 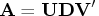 .
Take the reciprocals of significant singular
values and set the small values of
.
Take the reciprocals of significant singular
values and set the small values of 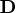 to zero.
to zero.
call svd(u,d,v,a); t = 1e-12 * d[1]; do i=1 to n; if d[i] < t then d[i] = 0.; else d[i] = 1. / d[i]; end; x1 = v * diag(d) * u` * b; len1 = x1` * x1; ss1 = ssq(a * x1 - b); x1 = x1`; print ss1 len1, x1 [format=best6.];The solution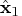 obtained by singular value
decomposition,
obtained by singular value
decomposition, 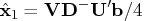 , is of minimum Euclidean length.
, is of minimum Euclidean length.
- Use QR decomposition with column pivoting:
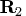 to zero and invert the upper
triangular matrix
to zero and invert the upper
triangular matrix 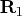 to obtain a generalized
inverse
to obtain a generalized
inverse 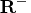 and an optimal solution
and an optimal solution 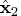 :
:
ord = j(n,1,0); call qr(qtb,r2,pivqr,lindqr,a,ord,b); nr = n - lindqr; r = r2[1:nr,1:nr]; x2 = shape(0,n,1); x2[pivqr] = trisolv(1,r,qtb[1:nr]) // j(lindqr,1,0.); len2 = x2` * x2; ss2 = ssq(a * x2 - b); x2 = x2`; print ss2 len2, x2 [format=best6.];Note that the residual sum of squares is minimal, but the solution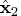 is not of minimum Euclidean length.
is not of minimum Euclidean length.
- Use the result
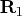 of the ROOT function on
this page to obtain the vector piv indicating
the zero rows in the upper triangular matrix
of the ROOT function on
this page to obtain the vector piv indicating
the zero rows in the upper triangular matrix 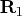 :
:
r1 = root(aa); nr = n - lind; piv = shape(0,n,1); j1 = 1; j2 = nr + 1; do i=1 to n; if r1[i,i] ^= 0 then do; piv[j1] = i; j1 = j1 + 1; end; else do; piv[j2] = i; j2 = j2 + 1; end; end;Now compute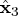 by solving the equation
by solving the equation
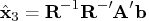 .
.
r = r1[piv[1:nr],piv[1:nr]]; x = trisolv(2,r,ab[piv[1:nr]]); x = trisolv(1,r,x); x3 = shape(0,n,1); x3[piv] = x // j(lind,1,0.); len3 = x3` * x3; ss3 = ssq(a * x3 - b); x3 = x3`; print ss3 len3, x3 [format=best6.];Note that the residual sum of squares is minimal, but the solution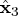 is not of minimum Euclidean length.
is not of minimum Euclidean length.
- Use the result
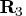 of the RUPDT call on
this page and the vector piv (obtained
in the previous solution), which indicates the zero
rows of upper triangular matrices
of the RUPDT call on
this page and the vector piv (obtained
in the previous solution), which indicates the zero
rows of upper triangular matrices 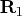 and
and 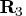 .
After zeroing out the rows of
.
After zeroing out the rows of 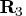 belonging
to small diagonal pivots, solve the system
belonging
to small diagonal pivots, solve the system
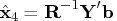 .
.
r3 = shape(0,n,n); qtb = shape(0,n,1); call rupdt(rup,bup,sup,r3,a,qtb,b); r3 = rup; qtb = bup; call rzlind(lind,r4,bup,r3,,qtb); qtb = bup[piv[1:nr]]; x = trisolv(1,r4[piv[1:nr],piv[1:nr]],qtb); x4 = shape(0,n,1); x4[piv] = x // j(lind,1,0.); len4 = x4` * x4; ss4 = ssq(a * x4 - b); x4 = x4`; print ss4 len4, x4 [format=best6.];Since the matrices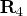 and
and 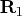 are the
same (except for the signs of rows), the solution
are the
same (except for the signs of rows), the solution
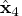 is the same as
is the same as 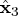 .
. - Use the result
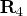 of the RZLIND call in the
previous solution, which is the result of the first
step of complete QR decomposition, and perform
the second step of complete QR decomposition.
The rows of matrix
of the RZLIND call in the
previous solution, which is the result of the first
step of complete QR decomposition, and perform
the second step of complete QR decomposition.
The rows of matrix 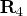 can be
permuted to the upper trapezoidal form
can be
permuted to the upper trapezoidal form
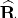 is nonsingular and
upper triangular and
is nonsingular and
upper triangular and 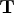 is rectangular.
Next, perform the second step of complete QR
decomposition with the lower triangular matrix
is rectangular.
Next, perform the second step of complete QR
decomposition with the lower triangular matrix
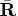 .
.
r = r4[piv[1:nr],]`; call qr(q,r5,piv2,lin2,r); y = trisolv(2,r5,qtb); x5 = q * (y // j(lind,1,0.)); len5 = x5` * x5; ss5 = ssq(a * x5 - b); x5 = x5`; print ss5 len5, x5 [format=best6.];
The solution obtained by complete
QR decomposition has minimum Euclidean length.
obtained by complete
QR decomposition has minimum Euclidean length.
- Perform both steps of complete QR decomposition.
The first step performs the pivoted QR decomposition of
 ,
,
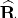 is nonsingular and
upper triangular and
is nonsingular and
upper triangular and 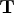 is rectangular.
The second step performs a QR decomposition
as described in the previous method.
This results in
is rectangular.
The second step performs a QR decomposition
as described in the previous method.
This results in
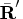 is lower triangular.
is lower triangular.
ord = j(n,1,0); call qr(qtb,r2,pivqr,lindqr,a,ord,b); nr = n - lindqr; r = r2[1:nr,]`; call qr(q,r5,piv2,lin2,r); y = trisolv(2,r5,qtb[1:nr]); x6 = shape(0,n,1); x6[pivqr] = q * (y // j(lindqr,1,0.)); len6 = x6` * x6; ss6 = ssq(a * x6 - b); x6 = x6`; print ss6 len6, x6 [format=best6.];The solution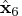 obtained by complete
QR decomposition has minimum Euclidean length.
obtained by complete
QR decomposition has minimum Euclidean length.
- Perform complete QR decomposition
with the QR and LUPDT calls:
ord = j(n,1,0); call qr(qtb,r2,pivqr,lindqr,a,ord,b); nr = n - lindqr; r = r2[1:nr,1:nr]`; z = r2[1:nr,nr+1:n]`; call lupdt(lup,bup,sup,r,z); rd = trisolv(3,lup,r2[1:nr,]); rd = trisolv(4,lup,rd); x7 = shape(0,n,1); x7[pivqr] = rd` * qtb[1:nr,]; len7 = x7` * x7; ss7 = ssq(a * x7 - b); x7 = x7`; print ss7 len7, x7 [format=best6.];The solution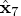 obtained by complete
QR decomposition has minimum Euclidean length.
obtained by complete
QR decomposition has minimum Euclidean length.
- Perform complete QR decomposition with
the RUPDT, RZLIND, and LUPDT calls:
r3 = shape(0,n,n); qtb = shape(0,n,1); call rupdt(rup,bup,sup,r3,a,qtb,b); r3 = rup; qtb = bup; call rzlind(lind,r4,bup,r3,,qtb); nr = n - lind; qtb = bup; r = r4[piv[1:nr],piv[1:nr]]`; z = r4[piv[1:nr],piv[nr+1:n]]`; call lupdt(lup,bup,sup,r,z); rd = trisolv(3,lup,r4[piv[1:nr],]); rd = trisolv(4,lup,rd); x8 = shape(0,n,1); x8 = rd` * qtb[piv[1:nr],]; len8 = x8` * x8; ss8 = ssq(a * x8 - b); x8 = x8`; print ss8 len8, x8 [format=best6.];The solution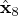 obtained by complete
QR decomposition has minimum Euclidean length.
The same result can be obtained
with the APPCORT or COMPORT call.
obtained by complete
QR decomposition has minimum Euclidean length.
The same result can be obtained
with the APPCORT or COMPORT call.
You can use various methods to compute the Moore-Penrose inverse
- Use the GINV operator.
The GINV operator in IML uses the singular
decomposition
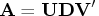 .
The result
.
The result 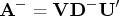 should be
identical to the result given by the next solution.
should be
identical to the result given by the next solution.
ga = ginv(a); t1 = a * ga; t2 = t1`; t3 = ga * a; t4 = t3`; ss1 = ssq(t1 - t2) + ssq(t3 - t4) + ssq(t1 * a - a) + ssq(t3 * ga - ga); print ss1, ga [format=best6.]; - Use singular value decomposition.
The singular decomposition
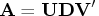 with
with 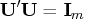 ,
, 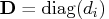 ,
and
,
and 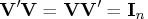 , can be
used to compute
, can be
used to compute 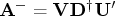 ,
with
,
with 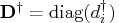 and
and
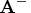 should be the same as that
given by the GINV operator if the singularity
criterion
should be the same as that
given by the GINV operator if the singularity
criterion 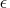 is selected correspondingly.
Since you cannot specify the criterion
is selected correspondingly.
Since you cannot specify the criterion 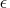 for the GINV operator, the singular value decomposition
approach can be important for applications where the
GINV operator uses an unsuitable
for the GINV operator, the singular value decomposition
approach can be important for applications where the
GINV operator uses an unsuitable 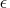 criterion.
The slight discrepancy between the values of
SS1 and SS2 is due to rounding that occurs
in the statement that computes the matrix GA.
criterion.
The slight discrepancy between the values of
SS1 and SS2 is due to rounding that occurs
in the statement that computes the matrix GA.
call svd(u,d,v,a); do i=1 to n; if d[i] <= 1e-10 * d[1] then d[i] = 0.; else d[i] = 1. / d[i]; end; ga = v * diag(d) * u`; t1 = a * ga; t2 = t1`; t3 = ga * a; t4 = t3`; ss2 = ssq(t1 - t2) + ssq(t3 - t4) + ssq(t1 * a - a) + ssq(t3 * ga - ga); print ss2;
- Use complete QR decomposition.
The complete QR decomposition
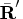 is lower
triangular, yields the Moore-Penrose inverse
is lower
triangular, yields the Moore-Penrose inverse
ord = j(n,1,0); call qr(q1,r2,pivqr,lindqr,a,ord); nr = n - lindqr; q1 = q1[,1:nr]; r = r2[1:nr,]`; call qr(q2,r5,piv2,lin2,r); tt = trisolv(4,r5`,q1`); ga = shape(0,n,m); ga[pivqr,] = q2 * (tt // shape(0,n-nr,m)); t1 = a * ga; t2 = t1`; t3 = ga * a; t4 = t3`; ss3 = ssq(t1 - t2) + ssq(t3 - t4) + ssq(t1 * a - a) + ssq(t3 * ga - ga); print ss3; - Use complete QR decomposition with QR and LUPDT:
ord = j(n,1,0); call qr(q,r2,pivqr,lindqr,a,ord); nr = n - lindqr; r = r2[1:nr,1:nr]`; z = r2[1:nr,nr+1:n]`; call lupdt(lup,bup,sup,r,z); rd = trisolv(3,lup,r2[1:nr,]); rd = trisolv(4,lup,rd); ga = shape(0,n,m); ga[pivqr,] = rd` * q[,1:nr]`; t1 = a * ga; t2 = t1`; t3 = ga * a; t4 = t3`; ss4 = ssq(t1 - t2) + ssq(t3 - t4) + ssq(t1 * a - a) + ssq(t3 * ga - ga); print ss4;
r3 = shape(0,n,n);
y = i(m); qtb = shape(0,n,m);
call rupdt(rup,bup,sup,r3,a,qtb,y);
r3 = rup; qtb = bup;
call rzlind(lind,r4,bup,r3,,qtb);
nr = n - lind; qtb = bup;
r = r4[piv[1:nr],piv[1:nr]]`;
z = r4[piv[1:nr],piv[nr+1:n]]`;
call lupdt(lup,bup,sup,r,z);
rd = trisolv(3,lup,r4[piv[1:nr],]);
rd = trisolv(4,lup,rd);
ga = shape(0,n,m);
ga = rd` * qtb[piv[1:nr],];
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss5 = ssq(t1 - t2) + ssq(t3 - t4) +
ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss5;
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
![[ \hat{{{r}}}^' \ {t}^' ] = \bar{{y}} [ \bar{{{r}}} \ 0 ]](images/langref_langrefeq1142.gif)