Language Reference: APPCORT Call :: SAS/IML(R) 9.2 User's Guide

Language Reference

APPCORT Call

applies complete orthogonal decomposition by Householder transformations on the right-hand-side matrix B for the solution of rank-deficient linear least squares systems

CALL APPCORT( prqb, lindep, 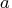, 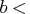$b\lt$ , sing>);

The inputs to the APPCORT subroutine are as follows:

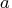
is an

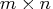matrix

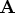, with 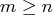$m \geq n$ , which is to be decomposed into the product of the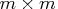

orthogonal matrix

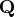, the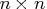

upper triangular matrix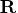

, and the

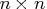orthogonal matrix

${a}= {q}[ {{r}}\ 0 ] {{{{\pi}}}}^' {p}^' {{{{\pi}}}}$

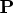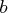
is the

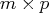matrix

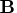that is to be left multiplied by the transposed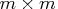

matrix ${q}^'$ .

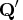sing

is an optional scalar specifying a singularity criterion.

The APPCORT subroutine returns the following values:

prqb

is an

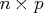matrix product

${p}{{{{\pi}}}}[ ({l}^')^{-1} & 0 \ 0 & 0 ] {q}^' {b}$

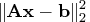which is the minimum 2-norm solution of the (rank deficient) least squares problem $\vert {a}{x}- {b}\vert^2_2$ . Refer to Golub and Van Loan (1989, pp. 241-242) for more details.

lindep

is the number of linearly dependent columns in the matrix

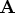detected by applying the

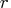Householder transformations. That is, lindep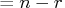

, where

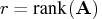See the section "COMPORT Call" for information about complete orthogonal decomposition.

An example that uses the APPCORT subroutine follows:

  
    /* Only four linearly independent columns */ 
    A = {1 0 1 0 0, 
         1 0 0 1 0, 
         1 0 0 0 1, 
         0 1 1 0 0, 
         0 1 0 1 0, 
         0 1 0 0 1 }; 
  
    /* compute Moore-Penrose generalized inverse */ 
    b = i(nrow(A)); 
    call appcort(Ainv,lindep,A,b); 
    print Ainv; 
  
    /* verify generalized inverse */ 
    eps = 1e-12; 
    if any(A*Ainv*A-A > eps) | 
       any(Ainv*A*Ainv-Ainv > eps) | 
       any((A*Ainv)`-A*Ainv > eps) | 
       any((Ainv*A)`-Ainv*A > eps) then 
           print "Pseudoinverse conditions not satisfied"; 
       else 
           print "Pseudoinverse conditions satisfied"; 
  
    /* compute solution for rank deficient LS: 
          min |Ax-b|^2 
       The range of A is a line. 
       b is a point not on the line. */ 
    A = { 1  2, 
          2  4, 
         -1 -2 }; 
    b = {1, 3, -2}; 
    call appcort(x,lindep,A,b); 
    print x; 
  
                                       AINV 
  
       0.2666667 0.2666667 0.2666667 -0.066667 -0.066667 -0.066667 
       -0.066667 -0.066667 -0.066667 0.2666667 0.2666667 0.2666667 
             0.4      -0.1      -0.1       0.4      -0.1      -0.1 
            -0.1       0.4      -0.1      -0.1       0.4      -0.1 
            -0.1      -0.1       0.4      -0.1      -0.1       0.4 
  
                       Pseudoinverse conditions satisfied 
  
                                        X 
  
                                          0.3 
                                          0.6

Top of Page