| Language Reference |
COMPORT Call
provides complete orthogonal decomposition by Householder transformations
- CALL COMPORT(
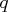 ,
, 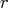 ,
, 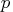 , piv, lindep,
, piv, lindep, 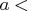 , b<,
sing>);
, b<,
sing>);
The COMPORT subroutine returns the following values:
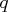
- If
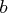 is not specified,
is not specified, 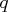 is the
is the 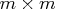 orthogonal matrix
orthogonal matrix 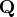 that is the product of the
that is the product of the
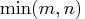 separate Householder transformations.
If
separate Householder transformations.
If 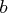 is specified,
is specified, 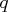 is the
is the 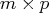 matrix
matrix 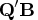 that has the transposed
Householder transformations
that has the transposed
Householder transformations 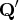 applied
on the
applied
on the 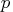 columns of the argument matrix
columns of the argument matrix 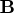 .
. 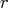
- is the
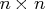 upper triangular matrix
upper triangular matrix 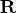 that
contains the
that
contains the 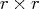 nonsingular upper triangular
matrix
nonsingular upper triangular
matrix 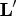 of the complete orthogonal
decomposition, where
of the complete orthogonal
decomposition, where 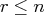 is the rank of
is the rank of  .
The full
.
The full 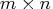 upper triangular matrix
upper triangular matrix 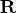 of the
orthogonal decomposition of matrix
of the
orthogonal decomposition of matrix  can be obtained
by vertical concatenation (IML operator //) of
the
can be obtained
by vertical concatenation (IML operator //) of
the 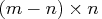 zero matrix to the result
zero matrix to the result 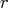 .
. - p
- is an
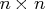 matrix that is the product
matrix that is the product 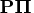 of a
permutation matrix
of a
permutation matrix 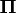 with an orthogonal matrix
with an orthogonal matrix
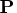 . The permutation matrix is determined by the vector piv.
. The permutation matrix is determined by the vector piv.
- piv
- is an
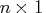 vector of permutations of the columns of
vector of permutations of the columns of  .
That is, the QR decomposition is computed, not of
.
That is, the QR decomposition is computed, not of  , but of
the matrix with columns
, but of
the matrix with columns ![[{a}_{piv[1]} ... {a}_{piv[n]}]](images/langref_langrefeq156.gif) .
The vector piv corresponds to an
.
The vector piv corresponds to an 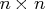 permutation matrix,
permutation matrix, 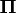 , of the pivoted QR
decomposition in the first step of orthogonal decomposition.
, of the pivoted QR
decomposition in the first step of orthogonal decomposition.
- lindep
- specifies the number of linearly dependent columns in the
matrix
 detected by applying the
detected by applying the 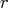 Householder
transformation in the order specified by the argument piv.
That is, lindep
Householder
transformation in the order specified by the argument piv.
That is, lindep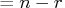 .
.
The inputs to the COMPORT subroutine are as follows:
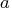
- specifies the
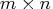 matrix
matrix  , with
, with 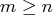 ,
which is to be decomposed into the product of the
,
which is to be decomposed into the product of the 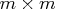 orthogonal matrix
orthogonal matrix 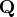 , the
, the 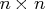 upper triangular
matrix
upper triangular
matrix 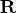 , and the
, and the 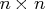 orthogonal matrix
orthogonal matrix 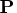 ,
,
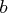
- specifies an optional
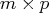 matrix
matrix
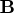 that is to be left multiplied by the
transposed
that is to be left multiplied by the
transposed 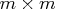 matrix
matrix 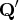 .
. - sing
- is an optional scalar specifying a singularity criterion.
The complete orthogonal decomposition of the singular matrix
- Use the QR decomposition of
 with column pivoting,
with column pivoting,
![{{r}}= [ {{r}}_1 & {{r}}_2 ] \in{\cal r}^{r x t}](images/langref_langrefeq161.gif) is upper trapezoidal,
is upper trapezoidal, 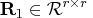 is upper triangular and invertible,
is upper triangular and invertible,
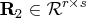 ,
,
![{q}= [{y}& {z}]](images/langref_langrefeq164.gif) is orthogonal,
is orthogonal,
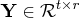 ,
,
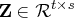 ,
and
,
and 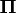 permutes the columns of
permutes the columns of  .
. - Use the transpose
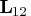 of the upper trapezoidal
matrix
of the upper trapezoidal
matrix ![{{r}}= [ {{r}}_1 & {{r}}_2 ]](images/langref_langrefeq168.gif) ,
,
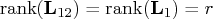 ,
,
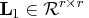 lower triangular,
lower triangular,
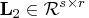 . The lower trapezoidal
matrix
. The lower trapezoidal
matrix 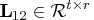 is premultiplied
with
is premultiplied
with 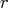 Householder transformations
Householder transformations  :
:
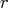 columns of
columns of
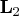 and producing the nonsingular lower
triangular matrix
and producing the nonsingular lower
triangular matrix 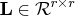 .
Therefore, you obtain
.
Therefore, you obtain
 and upper triangular
and upper triangular 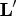 .
This second step is described in Golub
and Van Loan (1989, p. 220 and p. 236).
.
This second step is described in Golub
and Van Loan (1989, p. 220 and p. 236).
- Compute the Moore-Penrose inverse
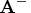 explicitly:
explicitly:
- (a)
- Obtain
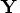 in
in ![{q}= [{y}& {z} ]](images/langref_langrefeq182.gif) explicitly by applying the
explicitly by applying the 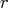 Householder
transformations obtained in the first step to
Householder
transformations obtained in the first step to
![[ {i}_r \ 0 ]](images/langref_langrefeq183.gif) .
.
- (b)
- Solve the
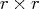 lower triangular system
lower triangular system
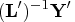 with
with 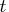 right-hand
sides by using backward substitution, which
yields an
right-hand
sides by using backward substitution, which
yields an 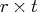 intermediate matrix.
intermediate matrix.
- (c)
- Left-apply the
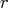 Householder transformations in
Householder transformations in
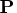 on the
on the 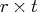 intermediate matrix
intermediate matrix
![[ ({l}^')^{-1}{y}^' \ 0 \ ]](images/langref_langrefeq187.gif) , which results in the
symmetric matrix
, which results in the
symmetric matrix 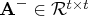 .
.
The GINV function computes the Moore-Penrose inverse
![]() by using the singular value decomposition of
by using the singular value decomposition of ![]() .
Using complete orthogonal decomposition to compute
.
Using complete orthogonal decomposition to compute
![]() usually requires far fewer floating-point operations.
However, it can be slightly more sensitive to rounding
errors, which can disturb the detection of the true
rank of
usually requires far fewer floating-point operations.
However, it can be slightly more sensitive to rounding
errors, which can disturb the detection of the true
rank of ![]() , than singular value decomposition.
, than singular value decomposition.
The following example demonstrates the use of the APPCORT subroutine, as well as the resulting output:
/* Only four linearly independent columns */
A = {1 0 1 0 0,
1 0 0 1 0,
1 0 0 0 1,
0 1 1 0 0,
0 1 0 1 0,
0 1 0 0 1 };
m = nrow(A);
n = ncol(A);
call comport(q,r,p,piv,lindep,A);
fullR = r // j(m-n, n, 0);
perm = i(n);
perm[piv,] = i(n);
/* recover A from factorization */
A2 = q*fullR*p`*perm`;
reset fuzz;
print A2;
/* compute Moore-Penrose generalized inverse */
rankA = n - lindep;
subR = R[1:rankA, 1:rankA];
fullRinv = j(n, n, 0);
fullRinv[1:rankA, 1:rankA] = inv(subR);
Ainv = perm*p*fullRinv*q[,1:n]`;
print Ainv;
/* verify generalized inverse */
eps = 1e-12;
if any(A*Ainv*A-A > eps) |
any(Ainv*A*Ainv-Ainv > eps) |
any((A*Ainv)`-A*Ainv > eps) |
any((Ainv*A)`-Ainv*A > eps) then
print "Pseudoinverse conditions not satisfied";
else
print "Pseudoinverse conditions satisfied";
A2
1 0 1 0 0
1 0 0 1 0
1 0 0 0 1
0 1 1 0 0
0 1 0 1 0
0 1 0 0 1
AINV
0.2666667 0.2666667 0.2666667 -0.066667 -0.066667 -0.066667
-0.066667 -0.066667 -0.066667 0.2666667 0.2666667 0.2666667
0.4 -0.1 -0.1 0.4 -0.1 -0.1
-0.1 0.4 -0.1 -0.1 0.4 -0.1
-0.1 -0.1 0.4 -0.1 -0.1 0.4
Pseudoinverse conditions satisfied
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.