| Language Reference |
QR Call
produces the QR decomposition of a matrix by Householder transformations
- CALL QR(
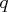 ,
, 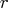 , piv, lindep,
, piv, lindep, 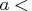 , ord<,
b>);
, ord<,
b>);
The QR subroutine returns the following values:
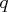
- specifies an orthogonal matrix
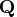 that is the product of
the Householder transformations applied to the
that is the product of
the Householder transformations applied to the 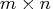 matrix
matrix  , if the
, if the 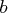 argument is not specified.
In this case, the
argument is not specified.
In this case, the 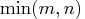 Householder transformations
are applied, and
Householder transformations
are applied, and 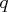 is an
is an 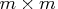 matrix.
If the
matrix.
If the 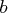 argument is specified,
argument is specified, 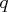 is the
is the 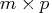 matrix
matrix 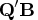 that has the transposed
Householder transformations
that has the transposed
Householder transformations 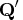 applied
on the
applied
on the 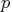 columns of the argument matrix
columns of the argument matrix 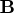 .
. 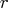
- specifies a
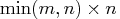 upper triangular
matrix
upper triangular
matrix 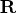 that is the upper part of the
that is the upper part of the
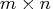 upper triangular matrix
upper triangular matrix 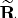 of the QR decomposition of the matrix
of the QR decomposition of the matrix  .
The matrix
.
The matrix 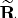 of the QR decomposition
can be obtained by vertical concatenation (by using the
IML operator //) of the
of the QR decomposition
can be obtained by vertical concatenation (by using the
IML operator //) of the 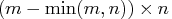 zero matrix to the result matrix
zero matrix to the result matrix 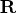 .
. - piv
- specifies an
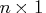 vector of permutations of the
columns of
vector of permutations of the
columns of  ; that is, on return, the QR decomposition
is computed, not of
; that is, on return, the QR decomposition
is computed, not of  , but of the permuted matrix
whose columns are
, but of the permuted matrix
whose columns are ![[{a}_{piv[1]} ... {a}_{piv[n]}]](images/langref_langrefeq156.gif) .
The vector piv corresponds to an
.
The vector piv corresponds to an
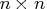 permutation matrix
permutation matrix 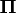 .
. - lindep
- is the number of linearly dependent columns in matrix
 detected by applying the
detected by applying the 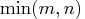 Householder transformations
in the order specified by the argument vector piv.
Householder transformations
in the order specified by the argument vector piv.
The inputs to the QR subroutine are as follows:
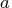
- specifies an
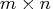 matrix
matrix  that is to be
decomposed into the product of the orthogonal matrix
that is to be
decomposed into the product of the orthogonal matrix
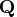 and the upper triangular matrix
and the upper triangular matrix 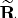 .
. - ord
- specifies an optional
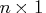 vector that
specifies the order of Householder transformations
applied to matrix
vector that
specifies the order of Householder transformations
applied to matrix  , as follows:
, as follows:
- ord
![[j{]} \gt 0](images/langref_langrefeq969.gif)
- Column
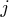 of
of  is an initial column, meaning it has to
be processed at the start in increasing order of ord
is an initial column, meaning it has to
be processed at the start in increasing order of ord![[j]](images/langref_langrefeq970.gif) .
. - ord
![[j{]} = 0](images/langref_langrefeq971.gif)
- Column
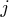 of
of  can be permuted in order
of decreasing residual Euclidean norm (pivoting).
can be permuted in order
of decreasing residual Euclidean norm (pivoting).
- ord
![[j{]} \lt 0](images/langref_langrefeq972.gif)
- Column
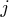 of
of  is a final column, meaning it has to
be processed at the end in decreasing order of ord
is a final column, meaning it has to
be processed at the end in decreasing order of ord![[j]](images/langref_langrefeq970.gif) .
.
![[j] = j](images/langref_langrefeq973.gif) , in which case the
Householder transformations are done in the same order that
the columns are stored in matrix
, in which case the
Householder transformations are done in the same order that
the columns are stored in matrix  (without pivoting).
(without pivoting).
- ord
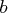
- specifies an optional
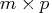 matrix
matrix 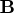 that is to be
multiplied by the transposed
that is to be
multiplied by the transposed 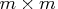 matrix
matrix 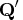 .
If
.
If 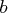 is specified, the result
is specified, the result 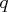 contains
the
contains
the 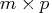 matrix
matrix 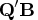 .
If
.
If 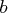 is not specified, the result
is not specified, the result 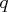 contains the
contains the 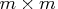 matrix
matrix 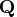 .
.
The QR subroutine decomposes an
The
call qr(q,r,piv,lindep,a,ord);
In many applications, the number of rows, In the usual case where
The
In the case where
Specifying the argument ord as an
- ord
![[j{]} \gt 0](images/langref_langrefeq969.gif) : Column
: Column 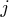 of
of  is an
initial column, meaning it has to be processed
at the start in increasing order of ord
is an
initial column, meaning it has to be processed
at the start in increasing order of ord![[j]](images/langref_langrefeq970.gif) .
This specification defines the first
.
This specification defines the first 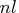 columns of
columns of  that are to be processed.
that are to be processed.
- ord
![[j{]} = 0](images/langref_langrefeq971.gif) : Column
: Column 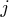 of
of  is a
pivot column, meaning it is to be processed
in order of decreasing residual Euclidean norms.
The pivot columns of
is a
pivot column, meaning it is to be processed
in order of decreasing residual Euclidean norms.
The pivot columns of  are processed
after the
are processed
after the 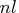 initial columns
and before the
initial columns
and before the 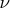 final columns.
final columns.
- ord
![[j{]} \lt 0](images/langref_langrefeq972.gif) : Column
: Column 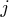 of
of  is a
final column, meaning it has to be processed
at the end in decreasing order of ord
is a
final column, meaning it has to be processed
at the end in decreasing order of ord![[j]](images/langref_langrefeq970.gif) .
This specification defines the last
.
This specification defines the last 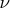 columns of
columns of  that are to be processed.
If
that are to be processed.
If 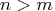 , some of these columns
will not be processed at all.
, some of these columns
will not be processed at all.
- If you do not specify the ord argument,
the default values ord
![[j] = j](images/langref_langrefeq973.gif) are used.
In this case, Householder transformations are
done in the same order in which the columns
are stored in
are used.
In this case, Householder transformations are
done in the same order in which the columns
are stored in  (without pivoting).
(without pivoting).
- If you set all components of ord to zero,
the Householder transformations are done in order of
decreasing Euclidean norms of the columns of
 .
.
To check the QR decomposition, use the following statements to compute the three residual sum of squares, represented by the variables SS0, SS1, and SS2, which should be close to zero:
m = nrow(a); n = ncol(a);
call qr(q,r,piv,lindep,a,ord);
ss0 = ssq(a[ ,piv] - q[,1:n] * r);
ss1 = ssq(q * q` - i(m));
ss2 = ssq(q` * q - i(m));
If the QR subroutine detects linearly dependent columns while processing matrix
The scalar result lindep counts the number of linearly dependent columns that are detected in constructing the first
Solving the linear system
call qr(qtb,r,piv,lindep,a,ord,b);
x[piv] = inv(r) * qtb[1:n,1:p];
The following example solves the full-rank linear least squares problem. Specify the argument
call qr(q,r,piv,lindep,a,ord,b);
When you specify the
a= { 36 -630 3360 -7560 7560 -2772,
-630 14700 -88200 211680 -220500 83160,
3360 -88200 564480 -1411200 1512000 -582120,
-7560 211680 -1411200 3628800 -3969000 1552320,
7560 -220500 1512000 -3969000 4410000 -1746360,
-2772 83160 -582120 1552320 -1746360 698544 };
b= { 463, -13860, 97020, -258720, 291060, -116424};
n = 5; aa = a[,1:n];
call qr(qtb,r,piv,lindep,aa,,b);
if lindep=0 then x=inv(r)*qtb[1:n];
print x;
Note that you are using only the first
if lindep=0 then x=trisolv(1,r,qtb[1:n],piv);
print x;
Both cases produce the following output:
X
1
0.5
0.3333333
0.25
0.2
For information about solving rank-deficient linear least squares problems, see the RZLIND call.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
![{a}= [ * & * & * \ {}* & * & * \ {}* & * & * \ {}* & * & * \ {}* & * & *... ... & 0 & * ] \ {q}= [ {q}_1 {q}_2 ], & & \widetilde{{{r}}} = [ {{r}}\ 0 ]](images/langref_langrefeq975.gif)
![{a}= [ * & * & * & * & * \ {}* & * & * & * & * \ {}* & * & * & * & * ] & &... ...} = {{r}}= [ * & * & * & * & * \ 0 & * & * & * & * \ 0 & 0 & * & * & * ]](images/langref_langrefeq978.gif)