Language Reference: TRISOLV Function :: SAS/IML(R) 9.2 User's Guide

Language Reference

TRISOLV Function

solves linear systems with triangular matrices

TRISOLV( code, 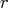, 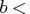$b\lt$ , piv>)

The TRISOLV function returns the following value:

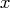
: is the 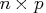matrix 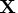containing 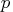solutions of the 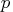linear systems specified by code, 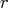, and .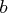

The inputs to the TRISOLV function are as follows:

code

specifies which of the following forms of triangular linear system has to be solved:

code=1: solve 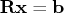, upper triangular
code=2: solve 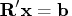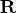${{r}}^' {x}= {b}$ , upper triangular
code=3: solve 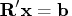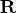${{r}}^' {x}= {b}$ , lower triangular
code=4: solve 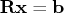, 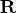lower triangular

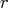
specifies the

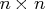nonsingular upper (code=1,2) or lower (code=3,4) triangular coefficient matrix

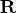. Only the upper or lower triangle of argument matrix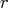

is used; the other triangle can contain any information.

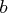
specifies the

matrix,

, of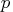

right-hand sides ${b}_k$ .

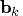piv

specifies an optional

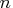vector that relates the order of the columns of matrix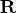

to the order of the columns of an original coefficient matrix

for which matrix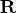

has been computed as a factor. For example, the vector piv can be the result of the QR decomposition of a matrix

whose columns were permuted in the order ${a}_{piv[1]}, ... , {a}_{piv[n]}$ .

For code=1 and code=3, the solution is obtained by backward elimination. For code=2 and code=4, the solution is obtained by forward substitution.

If TRISOLV recognizes the upper or lower triangular matrix as a singular matrix (that is, one that contains at least one zero diagonal element), it exits with an error message.

Consider the following example:

  
    R = { 1  0  0  0, 
          3  2  0  0, 
          1 -3  5  0, 
          2  7  9 -1 }; 
  
    b = {1, 1, 4, -6 }; 
    x = trisolv(4, R, b); 
    print x; 
  
  
  
                                X 
  
                                    1 
                                   -1 
                                    0 
                                    1

Also see the example in the QR call section.

Top of Page