The TIMESERIES Procedure

Correlation Analysis

Subsections:

Correlation analysis can be performed on the working series by specifying the OUTCORR= option or one of the PLOTS= options that are associated with correlation. The CORR statement enables you to specify options that are related to correlation analysis.

Autocovariance Statistics

LAGS

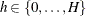
$h\in \{ 0, \ldots , H\} $

N

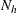$N_ h$ is the number of observed products at lag h, ignoring missing values

ACOV

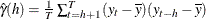
$\hat{\gamma }(h) = \frac{1}{T}\sum _{t=h+1}^{T} (y_ t - \overline{y}) (y_{t-h} - \overline{y})$

ACOV

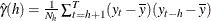$\hat{\gamma }(h) = \frac{1}{N_ h}\sum _{t=h+1}^{T} (y_ t - \overline{y}) (y_{t-h} - \overline{y})$ when embedded missing values are present

Autocorrelation Statistics

ACF

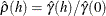
$\hat{\rho }(h)=\hat{\gamma }(h)/\hat{\gamma }(0)$

ACFSTD

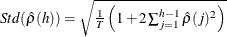
$Std(\hat{\rho }(h)) = \sqrt {\frac{1}{T}\left( 1 + 2 \sum _{j=1}^{h-1}\hat{\rho }(j)^2 \right)}$

ACFNORM

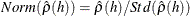
$Norm(\hat{\rho }(h)) = \hat{\rho }(h)/Std(\hat{\rho }(h))$

ACFPROB

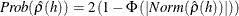
$Prob(\hat{\rho }(h)) = 2 \left( 1 - \Phi \left( |Norm(\hat{\rho }(h))| \right) \right)$

ACFLPROB

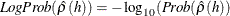
$LogProb(\hat{\rho }(h)) = -\log _{10} (Prob(\hat{\rho }(h))$

ACF2STD

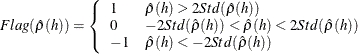
$Flag(\hat{\rho }(h)) = \left\{ \begin{array}{l l} 1 & \hat{\rho }(h) > 2Std(\hat{\rho }(h)) \\ 0 & -2Std(\hat{\rho }(h))< \hat{\rho }(h) < 2Std(\hat{\rho }(h)) \\ -1 & \hat{\rho }(h) < -2Std(\hat{\rho }(h)) \\ \end{array} \right.$

Partial Autocorrelation Statistics

PACF

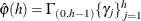
$\hat{\varphi }(h)=\Gamma _{(0, h-1)}\{ \gamma _ j\} ^ h_{j=1}$

PACFSTD

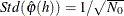
$Std(\hat{\varphi }(h)) = 1/\sqrt {N_0}$

PCFNORM

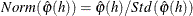
$Norm(\hat{\varphi }(h)) = \hat{\varphi }(h)/Std(\hat{\varphi }(h))$

PACFPROB

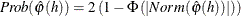
$Prob(\hat{\varphi }(h)) = 2 \left( 1 - \Phi \left( |Norm(\hat{\varphi }(h))| \right) \right)$

PACFLPROB

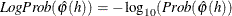
$LogProb(\hat{\varphi }(h)) = -\log _{10} (Prob(\hat{\varphi }(h))$

PACF2STD

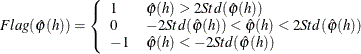
$Flag(\hat{\varphi }(h)) = \left\{ \begin{array}{l l} 1 & \hat{\varphi }(h) > 2Std(\hat{\varphi }(h)) \\ 0 & -2Std(\hat{\varphi }(h))< \hat{\varphi }(h) < 2Std(\hat{\varphi }(h)) \\ -1 & \hat{\varphi }(h) < -2Std(\hat{\varphi }(h)) \\ \end{array} \right.$

Inverse Autocorrelation Statistics

IACF

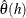
$\hat{\theta }(h)$

IACFSTD

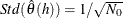
$Std(\hat{\theta }(h)) = 1/\sqrt {N_0}$

IACFNORM

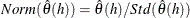
$Norm(\hat{\theta }(h)) = \hat{\theta }(h)/Std(\hat{\theta }(h))$

IACFPROB

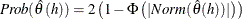
$Prob(\hat{\theta }(h)) = 2 \left( 1 - \Phi \left( |Norm(\hat{\theta }(h))| \right) \right)$

IACFLPROB

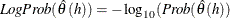
$LogProb(\hat{\theta }(h)) = -\log _{10} (Prob(\hat{\theta }(h))$

IACF2STD

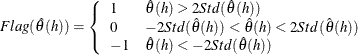
$Flag(\hat{\theta }(h)) = \left\{ \begin{array}{l l} 1 & \hat{\theta }(h) > 2Std(\hat{\theta }(h)) \\ 0 & -2Std(\hat{\theta }(h))< \hat{\theta }(h) < 2Std(\hat{\theta }(h)) \\ -1 & \hat{\theta }(h) < -2Std(\hat{\theta }(h)) \\ \end{array} \right.$

White Noise Statistics

WN

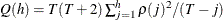
$Q(h) = T(T+2)\sum _{j=1}^ h \rho (j)^2/ (T-j)$

WN

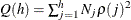$Q(h) = \sum _{j=1}^ h N_ j \rho (j)^2$ when embedded missing values are present

WNPROB

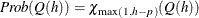
$Prob(Q(h)) = \chi _{\max (1, h-p)} (Q(h))$

WNLPROB

$LogProb(Q(h)) = -\log _{10} (Prob(Q(h))$