The TIMESERIES Procedure

Time Series Transformation

There are four transformations available for strictly positive series only. Let 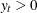${y_{t} > 0}$ be the original time series, and let 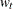${w_{t}}$ be the transformed series. The transformations are defined as follows:

Log

is the logarithmic transformation.

\[ w_{t} = \mr{ln}(y_{t}) \]
Logistic

is the logistic transformation.

\[ w_{t} = \mr{ln}(c y_{t} / (1-c y_{t})) \]

where the scaling factor ${c}$ is

\[ c = (1-10^{-6}) 10 ^{- \mr{ceil}( \mr{log}_{10}({max}( y_{t}) ))} \]

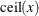and ${\mr{ceil}(x)}$ is the smallest integer greater than or equal to x.

Square root

is the square root transformation.

\[ w_{t} = \sqrt {y_{t}} \]
Box Cox

is the Box-Cox transformation.

\[ w_{t} = \begin{cases} \frac{y_{t}^{{\lambda }} - 1}{\lambda }, & {\lambda } {\ne } 0 \\ \mr{ln}(y_{t}), & {\lambda } = 0 \end{cases} \]

More complex time series transformations can be performed by using the EXPAND procedure of SAS/ETS.