The SSM Procedure (Experimental)

STATE Statement

STATE name (dim) <options> ;

The STATE statement specifies a subsection of $\pmb {\alpha }_{t}$ , the overall state vector at time . For more information, see the section State Space Model and Notation. Consider the state equations that define the state space model:

$\displaystyle \pmb {\alpha }_{t+1}$	$\displaystyle =$	$\displaystyle \mb {T}_{t} \pmb {\alpha }_{t} + \mb {c}_{t+1} + \pmb {\eta }_{t+1} \nonumber$
$\displaystyle \pmb {\alpha }_{1}$	$\displaystyle =$	$\displaystyle \mb {c}_{1} + \mb {A_{1}} \pmb {\delta } + \pmb {\eta }_{1} \nonumber$

You can specify multiple STATE statements, each specifying a separate subsection. It is assumed that the subsections specified by using different STATE statements are mutually independent. This independence assumption implies a block-diagonal structure for the transition matrices $\mb {T}_{t}$ and the disturbance covariances $\mb {Q}_{t}$ for all $t \geq 1$ . An appropriate block structure also applies to $\mb {A}_{1}$ . The options in the STATE statement provide complete control over the description of the relevant blocks of $\mb {T}_{t}$ , $\mb {Q}_{t}$ , and $\mb {A}_{1}$ . The argument dim (a positive integer in name (dim)) specifies the nominal dimension of this subsection. In most situations the nominal dimension and the actual dimension of the state subsection are the same. However, when you specify the TYPE= option, the actual dimension of the state subsection can be different than the nominal dimension. The TYPE= option simplifies the state specification task for some commonly needed models.

Note: The T, COV, and COV1 options described later in this section specify the relevant blocks of $\mb {T}_{t}$ , $\mb {Q}_{t}$ , and $\mb {Q}_{1}$ , respectively. The structure of these matrix blocks is described in a similar way in the option descriptions. For example, the specification COV(I) corresponds to the identity form, COV(D) corresponds to the diagonal form, and COV(G) corresponds to the general form of the $\mb {Q}_{t}$ block.

You can use the following options in the STATE statement to specify the system matrices $\mb {T}_{t}$ , $\mb {Q}_{t}$ , and $\mb {A}_{1}$ , and to request printing of their estimates:

A1(nd)

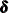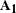specifies that the last nd elements of the state subsection be treated as diffuse. This becomes the dimension of the relevant subsection of the diffuse vector $\pmb {\delta }$ . The $\mb {A_{1}}$ block is created by using appropriate columns of the identity matrix. The value of nd must lie between 1 and the nominal dimension, dim. The absence of this option signifies that this subsection of 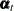$\pmb {\alpha }_{t}$ is nondiffuse. If both the COV1 and A1 options are specified, the last nd rows and columns of the matrix specified in the COV1 option are taken to be 0. This option cannot be used together with the RANK= option of the COV1 option.

COV( D ) <= (var1 var2 ...) | (number1 number2 ...)> COV( G ) <= (var1 var2 ...) | (number1 number2 ...)> COV( I ) <= (variable) | (number)> COV( RANK=integer )

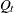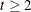specifies the relevant block of the disturbance covariance $Q_{t}$ (for $t \geq 2$ ) in the transition equation. Similar to the T option, the absence of this option signifies that this Q-block consists of only zeros. The structure of the Q-block is also similarly specified. However, the following differences exist:

The list that is specified to form the covariance must result in a symmetric, positive semidefinite matrix. For an example, see Example 27.5.
You can specify a rank constraint on the Q-block by specifying COV(RANK=integer), where the specified integer must lie between 1 and dim. A rank constraint is permissible only for the general form and only when its elements are not specified by using a list.
The convention of treating unset variables as structural zeros, which is used in specifying sparsity of the T-block, is not used in the Q-block specification. Whenever you explicitly specify the entries of the Q-block by specifying a list of variables in parentheses, all variables in the list must evaluate to nonmissing values.

The following examples illustrate different ways of specifying a Q-block. It is assumed that dim = 2.

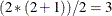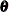COV(G) specifies a general-form Q-block, which contributes unspecified elements to the parameter vector $\pmb {\theta }$ .
COV(RANK=1) specifies a rank-one Q-block.

COV1( D ) <= (var1 var2 ...) | (number1 number2 ...)> COV1( G ) <= (var1 var2 ...) | (number1 number2 ...)> COV1( I ) <= (variable) | (number)> COV1( RANK=integer )

specifies the relevant block of the initial state covariance 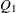$Q_{1}$ . The different options in this case have the same meaning as the options of the COV option. However, the following differences exist:

If the elements of 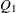$Q_{1}$ are specified by a list of variables in parentheses, then these variables must evaluate to constant values. In particular, they can depend on parameters that are specified by the PARMS statements; however, they cannot depend on any of the input data columns.
If the initial condition is partially diffuse (that is, the diffuse dimension nd specified in the A1 option is nonzero), the last nd rows and columns of the matrix specified in COV1 are taken to be zero. Moreover, if the elements of 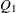$Q_{1}$ are specified by a list, its number of elements must correspond to a matrix of dimension (dim – nd).

PRINT=AR | COV | COV1 | MA | T PRINT=(<AR> <COV> <COV1> <MA> <T> )

requests printing of the respective system matrices. You can specify PRINT=AR or PRINT=MA only if you specify the TYPE=VARMA option. If any of these matrices are time-varying, the matrix that corresponds to the first time instance is printed.

SINPUT = (var1 var2 ...) | (number1 number2 ...)

specifies the relevant dim-dimensional block of the state input vector 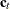$\mb {c}_{t}$ . The absence of this option signifies that this block of the 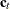$\mb {c}_{t}$ vector consists of only zeros. If the elements of 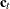$\mb {c}_{t}$ are specified by a list of variables in parentheses, then these variables must be independent of unknown parameters. In particular, they cannot be functions of parameters that are defined by the PARMS statements.

T( D ) <= (var1 var2 ...) | (number1 number2 ...)> T( G ) <= (var1 var2 ...) | (number1 number2 ...)> T( I ) <= (variable) | (number)>

specifies the relevant block of the transition matrix 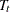$T_{t}$ . The absence of this option signifies that this block consists of only zeros. You can specify the structure of the T-block by specifying T(I) for the identity form, T(D) for the diagonal form, and T(G) for a general unstructured form. In addition, you can explicitly specify the entries of the T-block by specifying a list of numbers in parentheses, or by specifying in parentheses a list of variables that are defined by using the programming statements. The unspecified elements of the T-block are included in the list of parameters to be estimated from the data. If the elements of the T-block are supplied by a list in parentheses, the number of elements in the list depends on its structure. For the diagonal form, the list must contain exactly dim elements. In the case of the identity form—T(I)—the block is already fully specified; however, a specification T(I)=(variable) is understood to mean that the identity block is scaled by the specified variable (or a number). In the general case—T(G)—the list must consist of 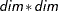$\Argument{dim}*\Argument{dim}$ elements, specified in a rowwise fashion. An inappropriate number of elements in the list results in a syntax error.

The following examples illustrate different ways of specifying the transition matrix. It is assumed that dim = 2.

T(I) specifies that the T-block is a two-dimensional identity matrix.
T(D) specifies that the T-block is a two-dimensional diagonal matrix. The two unspecified diagonal entries become part of the parameter vector $\pmb {\theta }$ .
T(D)=(1.1 2) fully specifies the two-dimensional diagonal T-block.
T(D)=( $X_{1} X_{2}$ ) specifies a two-dimensional diagonal T-block where the diagonal elements are dynamically calculated based on the values of the variables $X_{1}$ and $X_{2}$ . In this case the T-block can change with time if $X_{1}$ or $X_{2}$ changes with time.
T(G) specifies a general form T-block (with unspecified elements).
T(G)=( $X_{1} X_{2} X_{3} X_{4}$ ) specifies a general form T-block where the first row is formed by $X_{1}$ and $X_{2}$ , and the second row is formed by $X_{3}$ and $X_{4}$ .

In practice the transition matrix is often sparse—that is, many of its elements are 0. The algorithms in the SSM procedure exploit this sparsity structure for computational efficiency. Whenever you explicitly specify the entries of the T-block by specifying a list of variables in parentheses, you can leave the variables that correspond to the zero elements unset. These unset variables are treated as structural zeros by the SSM procedure. The section Sparse Transition Matrix Specification further explains how to use this sparsity convention.

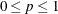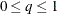specifies a state subsection that corresponds to the specified type. You can specify either a number or a variable for the RHO= and PERIOD= suboptions. When TYPE=VARMA, the autoregressive and moving average orders can be at most 1 ( $0 \leq p \leq 1$ and $0 \leq q \leq 1$ ). Moreover, by using the D and I flags with the order specification, you can impose additional structure on the autoregressive and moving average coefficient matrices—for example, specifying TYPE=VARMA(P=1) implies a VAR(1) model with general autoregressive coefficient matrix, whereas specifying TYPE=VARMA(P(D)=1) implies a VAR(1) model with diagonal autoregressive coefficient matrix. If you specify the TYPE= option, the T, COV1, SINPUT, and A1 options are not needed. 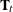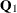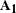In fact they are ignored, since the transition matrix $\mb {T}_{t}$ and the matrices in the initial condition ( $\mb {Q}_{1}$ and $\mb {A_{1}}$ ) are implicitly defined by the choice of the type. However, the specification of the COV option does play a key role in the eventual form of 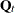$\mb {Q}_{t}$ —the covariance of the disturbance term in the transition equation. For the types LL, CYCLE, SEASON, and VARMA, the dimension of the resulting state subsection is a certain multiple of dim, the nominal dimension in the STATE statement. For example, the following specification results in a state subsection, named cycleState, of dimension 2*dim:

     state cycleState(dim) cov(g) type=cycle;

The name cycleState corresponds to the state underlying a dim-dimensional cycle component. All of these special state types require that the data be regular (replication is permissible); the only exception is TYPE=CYCLE(CT), which defines a continuous-time cycle and is applicable to any data type. Table 27.2 summarizes some of this information for easy reference. For more information about these state types, see the section Predefined Structural Models.

The TYPE=LL specification results in a state that corresponds to a multivariate local linear trend. It is governed by two covariance matrices: the COV option specifies the covariance that corresponds to the level equation, and the SLOPECOV suboption specifies the covariance used in the slope equation. The form of the SLOPECOV suboption is exactly the same as that of the COV option.

The TYPE=CYCLE option results in a state that corresponds to a (stochastic) cycle. By default, this cycle is assumed to be for the regular data type. If TYPE=CYCLE(CT), the resulting cycle is applicable to any data type. The CT option is available only for dim = 1; that is, only a univariate cycle is available for the irregular data type. The cycle specification depends on a covariance matrix and two numbers: the damping factor RHO and the cycle period PERIOD. The covariance can be specified by the COV option. The damping factor is specified by the RHO= suboption; its value must lie between 0.0 and 1.0. The cycle period can be specified by the PERIOD= suboption. If the CT option is not included, the period value must be larger than 2.0. On the other hand, if the CT option is included, its value must be strictly positive. If these parameters are not specified, they are estimated from the data.

Table 27.2: Summary of Predefined State Types

Type	Description	Parameters	State Dimension
WN	dim-variate white noise	COV	dim
RW	dim-variate random walk	COV	dim
LL	dim-variate local linear	COV, SLOPECOV	2*dim
SEASON(LENGTH=length)	dim-variate season	COV	(length–1)*dim
CYCLE	dim-variate cycle	COV, RHO, PERIOD	2*dim
VARMA(P=p Q=q)	dim-variate VARMA(p, q)	COV, AR, MA	dim*max( p, q+1)