The SSM Procedure (Experimental)
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Data OrganizationOverview of Model Specification SyntaxLikelihood, Filtering, and SmoothingContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Data OrganizationOverview of Model Specification SyntaxLikelihood, Filtering, and SmoothingContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Two-Way Random-Effects and Autoregressive Model for Panel DataBackcasting, Forecasting, and InterpolationSmoothing of Repeated Measures DataA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic PlotsVariable Bandwidth Smoothing
Bivariate Basic Structural Model Two-Way Random-Effects and Autoregressive Model for Panel DataBackcasting, Forecasting, and InterpolationSmoothing of Repeated Measures DataA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic PlotsVariable Bandwidth Smoothing - References
Computational Issues
A Well-Behaved Model
The model defined by the state space model equations (see the section State Space Model and Notation) is very general. This generality is quite useful because it encompasses a wide variety of data generation processes. On
the other hand, it also makes it easy to specify overly complex and numerically unstable models. If a suitable model is not
already known and you are in the early phases of modeling, it is important to start with models that are relatively simple
and well-behaved from the numerical standpoint. From the numerical and statistical considerations, two aspects of model formulation
are particularly important: identifiability and numerical stability. A model is identifiable if the observed data has a distinct
probability distribution for each admissible parameter vector. Unless proper care is taken, it is easy to specify an unidentifiable
state space model. Similarly, predictions according to some types of state space models can display explosive growth or wild
oscillations. This behavior is primarily governed by the transition matrix ![]() (or
(or ![]() in the time-varying case). Unidentifiable models can run into difficulties during parameter estimation, and explosive growth
(and wild oscillation) causes numerical problems associated with finite-precision arithmetic. Unfortunately, no simple identifiability
check is available for a general state space model, and it is difficult to decide at the outset whether a specified model
might suffer from numerical instability. See Harvey (1989, chap. 4, sec. 4) for a discussion of identifiability issues, and
see Harvey (1989, chap. 3, sec. 3) for a discussion of the stability properties of time-invariant state space models. The
following guidelines are likely to result in models that are identifiable and numerically stable:
in the time-varying case). Unidentifiable models can run into difficulties during parameter estimation, and explosive growth
(and wild oscillation) causes numerical problems associated with finite-precision arithmetic. Unfortunately, no simple identifiability
check is available for a general state space model, and it is difficult to decide at the outset whether a specified model
might suffer from numerical instability. See Harvey (1989, chap. 4, sec. 4) for a discussion of identifiability issues, and
see Harvey (1989, chap. 3, sec. 3) for a discussion of the stability properties of time-invariant state space models. The
following guidelines are likely to result in models that are identifiable and numerically stable:
-
Build models by composing submodels that are known to be well-behaved. The predefined models provided by the SSM procedure are good submodel candidates (see the sections Predefined Trend Models and Predefined Structural Models).
-
Pay careful attention to the way the variety of system matrices are defined. The behavior of their elements, as functions of model parameters and other variables, must be well-understood. If these elements are defined by using DATA steps, you can validate their behavior by running these DATA steps outside of the SSM procedure. In particular, note the following:
-
The transition matrix
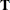 (or
(or 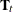 in the time-varying case) determines the explosiveness characteristics of the model; it must be well-behaved for all parameters.
in the time-varying case) determines the explosiveness characteristics of the model; it must be well-behaved for all parameters.
-
The disturbance covariances
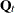 must be positive semidefinite for all parameters.
must be positive semidefinite for all parameters.
-
If the transition matrix
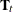 or the disturbance covariance
or the disturbance covariance 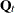 are time-varying and the data contain replicate observations (observations with the same ID value), check that the elements
of
are time-varying and the data contain replicate observations (observations with the same ID value), check that the elements
of 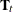 and
and 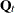 do not vary during replicate observations. This follows from the fact that the underlying state does not vary during replications
(see the state equation in the section State Space Model and Notation and the section Types of Data Organization).
do not vary during replicate observations. This follows from the fact that the underlying state does not vary during replications
(see the state equation in the section State Space Model and Notation and the section Types of Data Organization).
-
Convergence Problems
As explained in the section Likelihood Computation and Model Fitting Phase, the model parameters are estimated by nonlinear optimization of the likelihood. This process is not guaranteed to succeed. For some data sets, the optimization algorithm can fail to converge. Nonconvergence can result from a number of causes, including flat or ridged likelihood surfaces and ill-conditioned data. It is also possible for the algorithm to converge to a point that is not the global optimum of the likelihood.
If you experience convergence problems, consider the following:
-
Data that are extremely large or extremely small can adversely affect results because of the internal tolerances used during the filtering steps of the likelihood calculation. Rescaling the data can improve stability.
-
Examine your model for redundancies in the included components and regressors. The components or regressors that are nearly collinear to each other can cause the optimization process to become unstable.
-
Lack of convergence can indicate model misspecification such as unidentifiable model or a violation of the normality assumption.
Computer Resource Requirements
The computing resources required for the SSM procedure depend on several factors. The memory requirement for the procedure
is largely dependent on the number of observations to be processed and the size of the state vector underlying the specified
model. If ![]() denotes the sample size and
denotes the sample size and ![]() denotes the size of the state vector, the memory requirement for the smoothing phase of the Kalman filter is of the order
of
denotes the size of the state vector, the memory requirement for the smoothing phase of the Kalman filter is of the order
of ![]() bytes, ignoring the lower-order terms. If the smoothed component estimates are not needed, then the memory requirement is
of the order of
bytes, ignoring the lower-order terms. If the smoothed component estimates are not needed, then the memory requirement is
of the order of ![]() bytes. Besides
bytes. Besides ![]() and
and ![]() , the computing time for the parameter estimation depends on the size of the parameter vector
, the computing time for the parameter estimation depends on the size of the parameter vector ![]() and how many likelihood evaluations are needed to reach the optimum.
and how many likelihood evaluations are needed to reach the optimum.