The SSM Procedure (Experimental)
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Data OrganizationOverview of Model Specification SyntaxLikelihood, Filtering, and SmoothingContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Data OrganizationOverview of Model Specification SyntaxLikelihood, Filtering, and SmoothingContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Two-Way Random-Effects and Autoregressive Model for Panel DataBackcasting, Forecasting, and InterpolationSmoothing of Repeated Measures DataA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic PlotsVariable Bandwidth Smoothing
Bivariate Basic Structural Model Two-Way Random-Effects and Autoregressive Model for Panel DataBackcasting, Forecasting, and InterpolationSmoothing of Repeated Measures DataA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic PlotsVariable Bandwidth Smoothing - References
Overview of Model Specification Syntax
An SSM specification involves the description of the terms in the observation equation, the state transition equation, and
the initial condition. For example, the response variables, the predictor variables, and the elements of the state transition
matrix ![]() must somehow be specified. The SSM procedure syntax is designed so that little effort is needed to specify the more commonly
needed models, while a highly flexible language is available for specifying more complex models. Two syntax features help
achieve this goal: the ability to build a complex specification by combining simpler subspecifications, and a programming
language for creating lists of variables to be used later in the model specification.
must somehow be specified. The SSM procedure syntax is designed so that little effort is needed to specify the more commonly
needed models, while a highly flexible language is available for specifying more complex models. Two syntax features help
achieve this goal: the ability to build a complex specification by combining simpler subspecifications, and a programming
language for creating lists of variables to be used later in the model specification.
The SSM procedure statements can be divided into two classes:
-
programming statements, which are used to create lists of variables that can be used for a variety purposes (for example, as the elements of the model system matrices)
-
statements specific to the SSM procedure that formulate the state space model and control its other aspects such as the input data specification and the resulting output
Since the matrices involved in the model specification can be specified as lists of variables, which you separately create by using the programming statements, you can finely control all aspects of the model specification. These programming statements permit the use of most DATA step language features such as the conditional logic (IF-THEN-ELSE), array type variables, and all the mathematical functions available in the DATA step. You can also use programming statements to define predictor variables on the fly.
Building a Complex Model Specification
In addition to being able to specify the system matrices in a flexible way, you can also build a complex model specification
in a modular way by combining simpler subspecifications. Suppose that the state vector for the model to be specified is composed
of subsections that are statistically independent, which is a common scenario in practical modeling situations. For example,
suppose that ![]() can be divided into two disjoint subsections
can be divided into two disjoint subsections ![]() and
and ![]() , which are statistically independent. This entails a corresponding block-diagonal structure to the system matrices
, which are statistically independent. This entails a corresponding block-diagonal structure to the system matrices ![]() and
and ![]() that govern the state equations. In this case the term
that govern the state equations. In this case the term ![]() that appears in the observation equation also splits into the sum
that appears in the observation equation also splits into the sum ![]() for appropriately partitioned matrices
for appropriately partitioned matrices ![]() and
and ![]() . The model specification syntax of the SSM procedure makes building an SSM from such smaller pieces easy. Throughout this
chapter, the linear combinations of the state subsections (such as
. The model specification syntax of the SSM procedure makes building an SSM from such smaller pieces easy. Throughout this
chapter, the linear combinations of the state subsections (such as ![]() ) that appear in the observation equation are called components. An SSM specification in the SSM procedure is created by combining separate component specifications. In general, you specify
a component in two steps: first you define a state subsection
) that appear in the observation equation are called components. An SSM specification in the SSM procedure is created by combining separate component specifications. In general, you specify
a component in two steps: first you define a state subsection ![]() , and then you define a matching linear combination
, and then you define a matching linear combination ![]() . For some special components, such as some commonly needed trend components, you can combine these two steps into one keyword specification.
. For some special components, such as some commonly needed trend components, you can combine these two steps into one keyword specification.
The following list summarizes the (nonprogramming) SSM procedure syntax statements used for model specification:
-
The ID statement specifies the index variable (
 ). It is assumed that the data within each BY group are ordered (in ascending order) according to the ID variable. The SSM
procedure automatically creates a variable,
). It is assumed that the data within each BY group are ordered (in ascending order) according to the ID variable. The SSM
procedure automatically creates a variable, _ID_DELTA_, which contains the difference between the successive ID values. This variable is available for use by the programming statements to define time-varying system matrices. For example, in the case of SSMs used for modeling the longitudinal data, the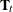 and
and 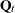 matrices often depend on
matrices often depend on _ID_DELTA_(see Example 27.5). -
The PARMS statement specifies variables that serve as the parameters of the model. That is, it partially defines the model parameter vector
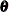 . Other elements of
. Other elements of  are implicitly defined if your specification of the system matrices is not fully complete.
are implicitly defined if your specification of the system matrices is not fully complete.
-
The STATE statement specifies a subsection of the model state vector. Multiple STATE statements can be used in the model specification; each one defines a statistically independent subsection of the model state vector. For full customization,
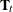 and
and 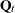 blocks that govern this subsection can be specified as lists of variables that are created by programming statements. However,
you can obtain many commonly needed state subsection types simply by using the TYPE= option in this statement. For example,
the use of TYPE=SEASON(LENGTH=12) results in a state subsection that can be used to define a monthly seasonal component.
blocks that govern this subsection can be specified as lists of variables that are created by programming statements. However,
you can obtain many commonly needed state subsection types simply by using the TYPE= option in this statement. For example,
the use of TYPE=SEASON(LENGTH=12) results in a state subsection that can be used to define a monthly seasonal component.
-
The COMPONENT statement specifies a linear combination that matches a state subsection that is previously defined in a STATE statement. Thus, a matching pair of STATE and COMPONENT statements define a component.
-
The TREND statement is used for easy specification of some commonly needed trend components.
-
The IRREGULAR statement specifies the observation disturbance for a particular response variable.
-
The MODEL statement specifies the observation equation for one of the response variables. A separate MODEL statement is needed for each response variable in the multivariate case. The MODEL statement specifies an equation in which the left-hand side is the response variable and the right-hand side is a list that contains components and regression variables.
Model Specification Steps
To illustrate the model specification steps, suppose y is a response variable and variables x1 and x2 are predictors. The following statements specify a model for y that includes two components named cycle and randomWalk, predictors x1 and x2, and an observation disturbance named whiteNoise:
parms lambda / lower=(1.e-6) upper=(3.14);
parms cycleVar / lower=(1.e-6);
array cycleT{4} c1-c4;
c1 = cos(lambda);
c2 = sin(lambda);
c3 = -c2;
c4 = c1;
state s_cycle(2) T(g)=(cycleT) cov(I)=(cycleVar) a1(2);
component cycle=(1 0)*s_cycle;
trend randomWalk(rw);
irregular whiteNoise;
model y = x1 x2 randomWalk cycle whiteNoise;
The specification begins with a PARMS statement that defines two parameters, lambda and cycleVar, along with their lower and upper bounds (essentially 0 and ![]() for
for lambda, and 0 and infinity for cycleVar). Next, programming statements define an array of variables, cycleT, which contains four variables, c1–c4; these variables are used later for defining the elements of the transition matrix of a state subsection. The STATE statement
specifies the two-dimensional subsection s_cycle; the dimension appears within the parentheses after the name (s_cycle(2)). The T= option specifies the transition matrix for the s_cycle (T(g)=(cycleT)); the g in T(g) signifies that the form of the T matrix is general. The COV= option (cov(I)=(cycleVar)) specifies the covariance of the state disturbance (![]() for
for ![]() ); because of the use of
); because of the use of I in cov(I), the covariance is of the form scaled identity, essentially a two-dimensional diagonal matrix with both diagonal elements
equal to cycleVar. The initial condition for s_cycle is completely diffuse because the A1= option, which specifies ![]() , specifies that the dimension of the diffuse vector
, specifies that the dimension of the diffuse vector ![]() is 2:
is 2: a1(2). In this case there is no need to specify the covariance ![]() in the initial condition. The COMPONENT statement specifies the component
in the initial condition. The COMPONENT statement specifies the component cycle. It specifies cycle as a dot product of two vectors—![]() and
and s_cycle, which merely selects the first element of s_cycle: component cycle=(1 0)*s_cycle. The TREND statement defines a component named randomWalk; its type is rw, which signifies random walk. The IRREGULAR statement defines an observation disturbance named whiteNoise. Both the randomWalk and whiteNoise specifications are only partially complete—for example, the disturbance variance of whiteNoise is not specified. These unspecified variances, trendVar, which corresponds to randomWalk, and wnVar, which corresponds to whiteNoise, are automatically included in the list of unknown parameters, ![]() , along with the parameters that are defined by the PARMS statements. Thus, the parameter vector for this model is
, along with the parameters that are defined by the PARMS statements. Thus, the parameter vector for this model is ![]() . Finally, the model specification is completed by the MODEL statement, which specifies the components of the observation
equation: the response variable
. Finally, the model specification is completed by the MODEL statement, which specifies the components of the observation
equation: the response variable y, the predictors x1 and x2, the components randomWalk and cycle, and the irregular term whiteNoise.
The preceding statements result in an SSM with a three-dimensional state vector, which is the result of combining the two-dimensional
state subsection, s_cycle, and a one-dimensional subsection underlying the trend, randomWalk. In this specification, the initial state is completely diffuse with ![]() a null matrix, and
a null matrix, and ![]() equal to the three-dimensional identity. The other state system matrices
equal to the three-dimensional identity. The other state system matrices ![]() and
and ![]() are time-invariant:
are time-invariant:
![\[ \mb {T} = \left[ \begin{tabular}{ccc} $\cos (\mr {lambda})$ & $ \sin (\mr {lambda})$ & 0 \\ $ -\sin (\mr {lambda})$ & $\cos (\mr {lambda})$ & 0 \\ 0 & 0 & 1 \end{tabular} \right] \; \; \mb {Q} = \left[ \begin{tabular}{ccc} cycleVar & 0 & 0 \\ 0 & cycleVar & 0 \\ 0 & 0 & trendVar \end{tabular} \right] \]](images/etsug_ssm0182.png) |
The observation equation is obvious with ![]() .
.
Sparse Transition Matrix Specification
It often happens that the transition matrix ![]() (or
(or ![]() in the time-varying case) specified in a STATE statement is sparse—that is, many of its elements are zero. The algorithms in the SSM procedure exploit this sparsity for
computational efficiency. In most cases the sparsity of a T-block can be inferred from the context. However, if the elements
of the T-block are supplied by a list of variables in parentheses, it can be difficult to recognize elements that are structurally
zero (this is because of the generality of the DATA step language used for defining the variables). To simplify the specification
of such sparse transition matrix, SSM procedure has adopted a convention: the variables that correspond to structural zeros
can (and should) be left unset—that is, these variables are declared, but no value is assigned to them. As an example, suppose that a three-dimensional
state subsection has the following form of transition matrix for some variables
in the time-varying case) specified in a STATE statement is sparse—that is, many of its elements are zero. The algorithms in the SSM procedure exploit this sparsity for
computational efficiency. In most cases the sparsity of a T-block can be inferred from the context. However, if the elements
of the T-block are supplied by a list of variables in parentheses, it can be difficult to recognize elements that are structurally
zero (this is because of the generality of the DATA step language used for defining the variables). To simplify the specification
of such sparse transition matrix, SSM procedure has adopted a convention: the variables that correspond to structural zeros
can (and should) be left unset—that is, these variables are declared, but no value is assigned to them. As an example, suppose that a three-dimensional
state subsection has the following form of transition matrix for some variables X1, X2, and X3 defined elsewhere in the program:
![\[ \mb {T} = \left[ \begin{tabular}{ccc} \Variable{X1} & 0 & 0 \\ \Variable{X2} & \Variable{X1} & 0 \\ \Variable{X3} & 0 & \Variable{X1} \end{tabular} \right] \]](images/etsug_ssm0185.png) |
The following (incomplete) statements show how to specify such a T-block:
array tMat{3,3};
do i=1 to 3;
tMat[i, i] = x1;
end;
tMat[2,1] = x2;
tMat[3,1] = x3;
state foo(3) T(g)=(tMat) ...;
In this specification only the nonzero elements of the tMat array, which contains ![]() elements, are assigned a value. On the other hand, the following statements show an alternate way of specifying the same
T-block. This specification explicitly sets the zeros in the T-block (the elements above the diagonal and
elements, are assigned a value. On the other hand, the following statements show an alternate way of specifying the same
T-block. This specification explicitly sets the zeros in the T-block (the elements above the diagonal and tMat[3,2]) to 0.
array tMat{3,3};
do i=1 to 3;
do j=1 to 3;
if i=j then tMat[i, j] = x1;
else if j > i then tMat[i, j] = 0;
end;
end;
tMat[2,1] = x2;
tMat[3,1] = x3;
tMat[3,2] = 0;
state foo(3) T(g)=(tMat) ...;
The first specification is simpler, and is preferred. The second specification is mathematically equivalent (and generates the same output) but is computationally less efficient since its sparsity structure cannot always be reliably inferred due to the generality of the DATA step language. In the first specification, the unset elements are recognized to be structural zeros while the set elements are treated as nonzero for sparsity purposes. See Example 27.5 for a simple illustration. Proper sparsity specification can lead to significant computational savings for larger matrices.
Regression Variable Specification in Multivariate Models
Suppose that a regression variable in a multivariate model affects two or more response variables. For example, suppose that
response variables y1 and y2 depend on a regression variable x. This dependence can be categorized as one of two types:
-
In the more common case, the regression coefficient of
xfory1and the regression coefficient ofxfory2are different. The relationship can be described as follows: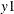
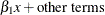
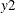
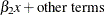
In the SSM procedure you can specify this type of relationship in two equivalent ways:
-
You can specify the variable
xin the MODEL statement fory1and specify the variablex_copy(a copy ofx) in the MODEL statement fory2as follows:x_copy = x; /* create a copy of x */ model y1 = x ...; model y2 = x_copy ...;
-
You can specify the variable
xin MODEL statements for bothy1andy2as follows:model y1 = x ...; model y2 = x ...;
This specification avoids creating
x_copy.
Of these two alternate ways, the first is preferred because
xandx_copycan then be unambiguously used in an EVAL statement to refer to the terms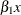 and
and 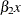 , respectively.
, respectively.
-
-
In the less common case,
y1andy2share a common regression coefficient.The relationship can be described as follows: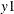
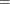
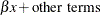
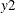
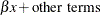
You can specify this type of relationship by placing the regression coefficient in the model state vector as follows:
state beta(1) T(I) A1(1) ; /* beta is a constant state */ comp xeffect = beta*(x) ; model y1 = xeffect ...; model y2 = xeffect ...;
Here the STATE statement defines
betaas a one-dimensional, time-invariant constant (because the transition matrix is identity, the disturbance covariance is 0 and the initial state is diffuse). Next, the COMP statement definesxeffectas the product betweenbetaand the variablex. Subsequently, bothy1andy2usexeffectin their respective MODEL statements.