The COPULA Procedure (Experimental)
- Overview
- Getting Started
-
Syntax

-
Details
 Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasCanonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names
Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasCanonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names -
Examples

- References
Archimedean Copulas
Overview of Archimedean Copulas
Let function ![]() be a strict Archimedean copula generator function and suppose its inverse
be a strict Archimedean copula generator function and suppose its inverse ![]() is completely monotonic on
is completely monotonic on ![]() . A strict generator is a decreasing function
. A strict generator is a decreasing function ![]() that satisfies
that satisfies ![]() and
and ![]() . A decreasing function
. A decreasing function ![]() is completely monotonic if it satisfies
is completely monotonic if it satisfies
|
|
An Archimedean copula is defined as follows:
|
|
The Archimedean copulas available in the COPULA procedure are the Clayton copula, the Frank copula, and the Gumbel copula.
Simulation
Suppose the generator of the Archimedean copula is ![]() . Then the simulation method using Laplace-Stieltjes transformation of the distribution function is given by Marshall and
Olkin (1988) where
. Then the simulation method using Laplace-Stieltjes transformation of the distribution function is given by Marshall and
Olkin (1988) where ![]() :
:
-
Generate a random variable
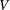 with the distribution function
with the distribution function 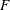 such that
such that 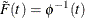 .
.
-
Draw samples from independent uniform random variables
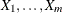 .
.
-
Return
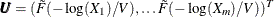 .
.
The Laplace-Stieltjes transformations are as follows:
-
For the Clayton copula,
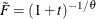 , and the distribution function
, and the distribution function 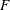 is associated with a Gamma random variable with shape parameter
is associated with a Gamma random variable with shape parameter 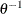 and scale parameter one.
and scale parameter one.
-
For the Gumbel copula,
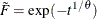 , and
, and 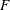 is the distribution function of the stable variable
is the distribution function of the stable variable 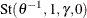 with
with ![$\gamma = [\cos (\pi /(2\theta ))]^\theta $](images/etsug_copula0149.png) .
.
-
For the Frank copula with
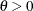 ,
, ![$\tilde{F}= - \log \{ 1-\exp (-t)[1- \exp (-\theta )]\} /\theta $](images/etsug_copula0150.png) , and
, and 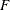 is a discrete probability function
is a discrete probability function 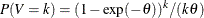 . This probability function is related to a logarithmic random variable with parameter value
. This probability function is related to a logarithmic random variable with parameter value 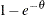 .
.
For details about simulating a random variable from a stable distribution, see Theorem 1.19 in Nolan (2010). For details about simulating a random variable from a logarithmic series, see Chapter 10.5 in Devroye (1986).
For a Frank copula with ![]() and
and ![]() , the simulation can be done through conditional distributions as follows:
, the simulation can be done through conditional distributions as follows:
-
Draw independent
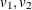 from a uniform distribution.
from a uniform distribution.
-
Let
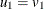 .
.
-
Let
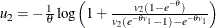 .
.
Fitting
One method to estimate the parameters is to calibrate with Kendall’s tau. The relation between the parameter ![]() and Kendall’s tau is summarized in the following table for the three Archimedean copulas.
and Kendall’s tau is summarized in the following table for the three Archimedean copulas.
Table 10.2: Calibration Using Kendall’s Tau
|
Copula Type |
|
Formula for |
|---|---|---|
|
Clayton |
|
|
|
Gumbel |
|
|
|
Frank |
|
No closed form |
In Table 10.2, ![]() for
for ![]() , and
, and ![]() for
for ![]() . In addition, for the Frank copula, the formula for
. In addition, for the Frank copula, the formula for ![]() has no closed form. The numerical algorithm for root finding can be used to invert the function
has no closed form. The numerical algorithm for root finding can be used to invert the function ![]() to obtain
to obtain ![]() as a function of
as a function of ![]() .
.
Alternatively, you can use the MLE or the CMLE method to estimate the parameter ![]() given the data
given the data ![]() and
and ![]() . The log-likelihood function for each type of Archimedean copula is provided in the following sections.
. The log-likelihood function for each type of Archimedean copula is provided in the following sections.
Fitting the Clayton Copula For the Clayton copula, the log-likelihood function is as follows (Cherubini, Luciano and Vecchiato 2004, Chapter 7):
|
|
|
|
|
|
Let ![]() be the derivative of
be the derivative of ![]() . Then the first order derivative is
. Then the first order derivative is
|
|
|
|
|
|
|
|
|
The second order derivative is
|
|
|
|
|
|
|
|
|
|
|
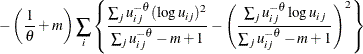 |
Fitting the Gumbel Copula
A different parameterization ![]() is used for the following part, which is related to the fitting of the Gumbel copula. For Gumbel copula, you need to compute
is used for the following part, which is related to the fitting of the Gumbel copula. For Gumbel copula, you need to compute
![]() . It turns out that for
. It turns out that for ![]() ,
,
|
|
where ![]() is a function that is described later. The copula density is given by
is a function that is described later. The copula density is given by
|
|
|
|
|
|
|
|
|
|
|
|
where ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,![]() , and
, and ![]() .
.
The log density is
|
|
|
|
|
|
|
|
Now the first order derivative of the log density has the decomposition
|
|
|
|
Some of the terms are given by
|
|
|
|
|
|
|
|
|
|
|
|
where
|
|
The last term in the derivative of the ![]() is
is
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Now the only remaining term is ![]() , which is related to
, which is related to ![]() . Wu, Valdez, and Sherris (2007) show that
. Wu, Valdez, and Sherris (2007) show that ![]() satisfies a recursive equation
satisfies a recursive equation
|
|
with ![]() .
.
The preceding equation implies that ![]() is a polynomial of
is a polynomial of ![]() and therefore can be represented as
and therefore can be represented as
|
|
In addition, its coefficient, denoted by ![]() , is a polynomial of
, is a polynomial of ![]() . For simplicity, use the notation
. For simplicity, use the notation ![]() . Therefore,
. Therefore,
|
|
|
|
|
|
|
|
Fitting the Frank copula
For the Frank copula,
|
|
When ![]() , a Frank copula has a probability density function
, a Frank copula has a probability density function
|
|
|
|
|
|
|
|
where ![]() .
.
The log likelihood is
|
|
Denote
|
|
Then the derivative of the log likelihood is
|
|
|
|
The term in the last summation is
|
|
|
|
The function ![]() satisfies a recursive relation
satisfies a recursive relation
|
|
with ![]() . Note that
. Note that ![]() is a polynomial whose coefficients do not depend on
is a polynomial whose coefficients do not depend on ![]() ; therefore,
; therefore,
|
|
|
|
|
|
|
|
|
|
|
|
where
|
|
|
|
|
|
For the case of ![]() and
and ![]() , the bivariate density is
, the bivariate density is
|
|
![\[ C_{\theta }(u_1, u_2,{\ldots }, u_ m) = \exp \left\{ - \left[ \sum _{i=1}^{m}(-\log u_ i)^\theta \right] ^{1/{\theta }} \right\} \]](images/etsug_copula0138.png)