The COPULA Procedure (Experimental)
- Overview
- Getting Started
-
Syntax

-
Details
 Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasCanonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names
Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasCanonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names -
Examples

- References
Sklar’s Theorem
The copula models are tools for studying the dependence structure of multivariate distributions. The usual joint distribution
function contains the information both about the marginal behavior of the individual random variables and about the dependence
structure between the variables. The copula is introduced to decouple the marginal properties of the random variables and
the dependence structures. A ![]() -dimensional copula is a joint distribution function on
-dimensional copula is a joint distribution function on ![]() with all marginal distributions being standard uniform. The common notation for a copula is
with all marginal distributions being standard uniform. The common notation for a copula is ![]() .
.
The Sklar (1959) theorem shows the importance of copulas in modeling multivariate distributions. The first part claims that a copula can be derived from any joint distribution functions, and the second part asserts the opposite: that is, any copula can be combined with any set of marginal distributions to result in a multivariate distribution function.
-
Let
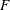 be a joint distribution function and
be a joint distribution function and  be the marginal distributions. Then there exists a copula
be the marginal distributions. Then there exists a copula ![$C: [0,1]^ m \rightarrow [0,1] $](images/etsug_copula0011.png) such that
such that
![\[ F(x_1,\ldots ,x_ m)= C(F_1(x_1),\ldots ,F_ m(x_ m)) \]](images/etsug_copula0012.png)
for all
 in
in ![$[-\infty ,\infty ]$](images/etsug_copula0014.png) . Moreover, if the margins are continuous, then
. Moreover, if the margins are continuous, then  is unique; otherwise
is unique; otherwise  is uniquely determined on
is uniquely determined on  , where
, where ![$\textrm{Ran}F_ j =F_ j([-\infty ,\infty ])$](images/etsug_copula0017.png) is the range of
is the range of  .
.
-
The converse is also true. That is, if
 is a copula and
is a copula and  are univariate distribution functions, then the multivariate function defined in the preceding equation is a joint distribution
function with marginal distributions
are univariate distribution functions, then the multivariate function defined in the preceding equation is a joint distribution
function with marginal distributions  .
.