The COPULA Procedure (Experimental)
- Overview
- Getting Started
-
Syntax

-
Details
 Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasCanonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names
Sklar’s TheoremDependence MeasuresNormal CopulaStudent’s t copulaArchimedean CopulasCanonical Maximum Likelihood Estimation (CMLE)Exact Maximum Likelihood Estimation (MLE)Calibration EstimationNonlinear Optimization OptionsDisplayed OutputOUTCOPULA= Data SetOUTPSEUDO=, OUT=, and OUTUNIFORM= Data SetsODS Table NamesODS Graph Names -
Examples

- References
Student’s t copula
Let ![]() and let
and let ![]() be a univariate t distribution with
be a univariate t distribution with ![]() degrees of freedom.
degrees of freedom.
The Student’s t copula can be written as
|
|
where ![]() is the multivariate Student’s t distribution with a correlation matrix
is the multivariate Student’s t distribution with a correlation matrix ![]() with
with ![]() degrees of freedom.
degrees of freedom.
Simulation
The input parameters for the simulation are ![]() . The
. The ![]() copula can be simulated by the following the two steps:
copula can be simulated by the following the two steps:
-
Generate a multivariate vector
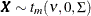 following the centered t distribution with
following the centered t distribution with  degrees of freedom and correlation matrix
degrees of freedom and correlation matrix 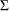 .
.
-
Transform the vector
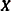 into
into 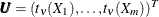 , where
, where 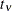 is the distribution function of univariate t distribution with
is the distribution function of univariate t distribution with  degrees of freedom.
degrees of freedom.
To simulate centered multivariate t random variables, you can use the property that ![]() if
if ![]() , where
, where ![]() and the univariate random variable
and the univariate random variable ![]() .
.
Fitting
To fit a ![]() copula is to estimate the covariance matrix
copula is to estimate the covariance matrix ![]() anddegrees of freedom
anddegrees of freedom ![]() from a given multivariate data set. Given a random sample
from a given multivariate data set. Given a random sample![]() ,
, ![]() that has uniform marginal distributions, the log likelihood is
that has uniform marginal distributions, the log likelihood is
|
|
|
|
|
|
where ![]() denotes the degrees of freedom of the t copula,
denotes the degrees of freedom of the t copula, ![]() denotes the joint density function of the centered multivariate t distribution with parameters
denotes the joint density function of the centered multivariate t distribution with parameters ![]() ,
, ![]() is the distribution function of a univariate t distribution with
is the distribution function of a univariate t distribution with ![]() degrees of freedom,
degrees of freedom, ![]() is a correlation matrix, and
is a correlation matrix, and ![]() is the density function of univariate t distribution with
is the density function of univariate t distribution with ![]() degrees of freedom.
degrees of freedom.
The log likelihood can be maximized with respect to the parameters ![]() using numerical optimization. If you allow the parameters in
using numerical optimization. If you allow the parameters in ![]() to be such that
to be such that ![]() is symmetric and with ones on the diagonal, then the MLE estimate for
is symmetric and with ones on the diagonal, then the MLE estimate for ![]() might not be positive semidefinite. In that case, you need to apply the adjustment to convert the estimated matrix to positive
semidefinite, as shown by McNeil, Frey, and Embrechts (2005), Algorithm 5.55.
might not be positive semidefinite. In that case, you need to apply the adjustment to convert the estimated matrix to positive
semidefinite, as shown by McNeil, Frey, and Embrechts (2005), Algorithm 5.55.
When the dimension of the data ![]() increases, the numerical optimization quickly becomes infeasible. It is common practice to estimate the correlation matrix
increases, the numerical optimization quickly becomes infeasible. It is common practice to estimate the correlation matrix
![]() by calibration using Kendall’s tau. Then, using this fixed
by calibration using Kendall’s tau. Then, using this fixed ![]() , the single parameter
, the single parameter ![]() can be estimated by MLE. By proposition 5.37 in McNeil, Frey, and Embrechts (2005),
can be estimated by MLE. By proposition 5.37 in McNeil, Frey, and Embrechts (2005),
|
|
where ![]() is the Kendall’s tau and
is the Kendall’s tau and ![]() is the off-diagonal elements of the correlation matrix
is the off-diagonal elements of the correlation matrix ![]() of the t copula. Therefore, an estimate for the correlation is
of the t copula. Therefore, an estimate for the correlation is
|
|
where ![]() and
and ![]() are the estimates of the sample correlation matrix and Kendall’s tau, respectively. However, it is possible that the estimate
of the correlation matrix
are the estimates of the sample correlation matrix and Kendall’s tau, respectively. However, it is possible that the estimate
of the correlation matrix ![]() is not positive definite. In this case, there is a standard procedure that uses the eigenvalue decomposition to transform
the correlation matrix into one that is positive definite. Let
is not positive definite. In this case, there is a standard procedure that uses the eigenvalue decomposition to transform
the correlation matrix into one that is positive definite. Let ![]() be a symmetric matrix with ones on the diagonal, with off-diagonal entries in
be a symmetric matrix with ones on the diagonal, with off-diagonal entries in ![]() . If
. If ![]() is not positive semidefinite, use Algorithm 5.55 from McNeil, Frey, and Embrechts (2005):
is not positive semidefinite, use Algorithm 5.55 from McNeil, Frey, and Embrechts (2005):
-
Compute the eigenvalue decomposition
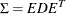 , where
, where 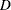 is a diagonal matrix that contains all the eigenvalues and
is a diagonal matrix that contains all the eigenvalues and 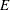 is an orthogonal matrix that contains the eigenvectors.
is an orthogonal matrix that contains the eigenvectors.
-
Construct a diagonal matrix
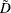 by replacing all negative eigenvalues in
by replacing all negative eigenvalues in 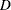 by a small value
by a small value 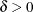 .
.
-
Compute
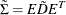 , which is positive definite but not necessarily a correlation matrix.
, which is positive definite but not necessarily a correlation matrix.
-
Apply the normalizing operator
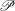 on the matrix
on the matrix 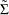 to obtain the correlation matrix desired.
to obtain the correlation matrix desired.
The log likelihood function and its gradient function for a single observation are listed as follows, where ![]() , with
, with ![]() , and
, and ![]() is the derivative of the
is the derivative of the ![]() function:
function:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The derivative of the likelihood with respect to the correlation matrix ![]() follows:
follows:
|
|
|
|
|
|