The TCOUNTREG Procedure (Experimental)
- Overview
- Getting Started
-
Syntax

-
Details
 Specification of Regressors Missing Values Poisson Regression Negative Binomial Regression Zero-Inflated Count Regression Overview Zero-Inflated Poisson Regression Zero-Inflated Negative Binomial Regression Variable Selection Panel Data Analysis Computational Resources Nonlinear Optimization Options Covariance Matrix Types Displayed Output OUTPUT OUT= Data Set OUTEST= Data Set ODS Table Names
Specification of Regressors Missing Values Poisson Regression Negative Binomial Regression Zero-Inflated Count Regression Overview Zero-Inflated Poisson Regression Zero-Inflated Negative Binomial Regression Variable Selection Panel Data Analysis Computational Resources Nonlinear Optimization Options Covariance Matrix Types Displayed Output OUTPUT OUT= Data Set OUTEST= Data Set ODS Table Names -
Examples

- References
| Specification of Regressors |
Each term in a model, called regressor, is a variable or combination of variables. Regressors are specified with a special notation that uses variable names and operators. There are two kinds of variables: classification (CLASS) variables and continuous variables. There are two primary operators: crossing and nesting. A third operator, the bar operator, is used to simplify effect specification.
In the SAS System, classification ( CLASS) variables are declared in the CLASS statement. (They can also be called categorical, qualitative, discrete, or nominal variables.) Classification variables can be either numeric or character. The values of a classification variable are called levels. For example, the classification variable Sex has the levels "male" and "female."
In a model, an independent variable that is not declared in the CLASS statement is assumed to be continuous. Continuous variables, which must be numeric, are used for covariates. For example, the heights and weights of subjects are continuous variables. A response variable is a discrete count variable and must also be numeric.
Types of Regressors
Seven different types of regressors are used in the TCOUNTREG procedure. In the following list, assume that A, B, C, D, and E are CLASS variables and that X1 and X2 are continuous variables:
Regressors are specified by writing continuous variables by themselves: X1 X2.
Polynomial regressors are specified by joining (crossing) two or more continuous variables with asterisks: X1*X1 X1*X2.
Dummy regressors are specified by writing CLASS variables by themselves: A B C.
Dummy interactions are specified by joining classification variables with asterisks: A*B B*C A*B*C.
Nested regressors are specified by following a dummy variable or dummy interaction with a classification variable or list of classification variables enclosed in parentheses. The dummy variable or dummy interaction is nested within the regressor listed in parentheses: B(A) C(B*A) D*E(C*B*A). In this example, B(A) is read "B nested within A."
Continuous-by-class regressors are written by joining continuous variables and classification variables with asterisks: X1*A.
Continuous-nesting-class regressors consist of continuous variables followed by a classification variable interaction enclosed in parentheses: X1(A) X1*X2(A*B).
One example of the general form of an effect that involves several variables is
This example contains an interaction of continuous terms with classification terms that are nested within more than one classification variable. The continuous list comes first, followed by the dummy list, followed by the nesting list in parentheses. Note that asterisks can appear within the nested list but not immediately before the left parenthesis.
The MODEL statement and several other statements use these effects. Some examples of MODEL statements that use various kinds of effects are shown in the following table, where a, b, and c represent classification variables. Variables x and z are continuous.
Specification |
Type of Model |
model y=x; |
Simple regression |
model y=x z; |
Multiple regression |
model y=x x*x; |
Polynomial regression |
model y=a; |
Regression with one classification variable |
model y=a b c; |
Regression with multiple classification variables |
model y=a b a*b; |
Regression with classification variables and their interactions |
model y=a b(a) c(b a); |
Regression with classification variables and their interactions |
model y=a x; |
Regression with both countibuous and classification variables |
model y=a x(a); |
Separate-slopes regression |
model y=a x x*a; |
Homogeneity-of-slopes regression |
The Bar Operator
You can shorten the specification of a large factorial model by using the bar operator. For example, two ways of writing the model for a full three-way factorial model follow:
model Y = A B C A*B A*C B*C A*B*C; model Y = A|B|C;
When the bar (|) is used, the right and left sides become effects, and the cross of them becomes an effect. Multiple bars are permitted. The expressions are expanded from left to right, using rules 2–4 given in Searle (1971, p. 390).
-
Multiple bars are evaluated from left to right. For instance, A|B|C is evaluated as follows:
A | B | C
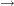
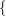 A | B
A | B 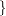 | C
| C 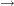
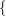 A B A*B
A B A*B 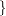 | C
| C 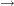
A B A*B C A*C B*C A*B*C
Crossed and nested groups of variables are combined. For example, A(B) | C(D) generates A*C(B D), among other terms.
Duplicate variables are removed. For example, A(C) | B(C) generates A*B(C C), among other terms, and the extra C is removed.
Effects are discarded if a variable occurs on both the crossed and nested parts of an effect. For instance, A(B) | B(D E) generates A*B(B D E), but this effect is eliminated immediately.
You can also specify the maximum number of variables involved in any effect that results from bar evaluation by specifying that maximum number, preceded by an @ sign, at the end of the bar effect. For example, the specification A | B | C@2 would result in only those effects that contain two or fewer variables: in this case, A B A*B C A*C and B*C.
More examples of using the | and @ operators follow:
A | C(B) |
is equivalent to |
A C(B) A*C(B) |
A(B) | C(B) |
is equivalent to |
A(B) C(B) A*C(B) |
A(B) | B(D E) |
is equivalent to |
A(B) B(D E) |
A | B(A) | C |
is equivalent to |
A B(A) C A*C B*C(A) |
A | B(A) | C@2 |
is equivalent to |
A B(A) C A*C |
A | B | C | D@2 |
is equivalent to |
A B A*B C A*C B*C D A*D B*D C*D |
A*B(C*D) |
is equivalent to |
A*B(C D) |
Note: This procedure is experimental.