Likelihood-Based Statistics

Let 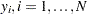denote the response variable values. Let 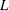be the likelihood as defined in the section Likelihood Function. Let denote the number of model parameters estimated. Note that 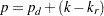, where 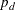is the number of distribution parameters, 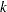is the number of regressors, if any, specified in the MODEL statement, and 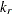is the number of regressors found to be linearly dependent (redundant) on other regressors. Given this notation, the likelihood-based statistics are defined as follows:

Neg2LogLike

The log likelihood is reported as

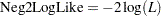
The multiplying factor 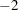makes it easy to compare it to the other likelihood-based statistics. A model with a smaller value of Neg2LogLike is deemed better.

AIC

The Akaike’s information criterion (AIC) is defined as

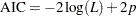
A model with a smaller value of AIC is deemed better.

AICC

The corrected Akaike’s information criterion (AICC) is defined as

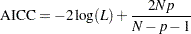
A model with a smaller value of AICC is deemed better. It corrects the finite-sample bias that AIC has when 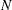is small compared to . AICC is related to AIC as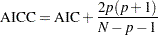

As 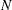becomes large compared to , AICC converges to AIC. AICC is usually recommended over AIC as a model selection criterion.

BIC

The Schwarz Bayesian information criterion (BIC) is defined as

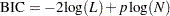
A model with a smaller value of BIC is deemed better.

EDF-Based Statistics

This class of statistics is based on the difference between the estimate of the cumulative distribution function (CDF) and the estimate of the empirical distribution function (EDF). Let 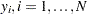denote the sample of 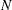values of the response variable. Let 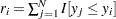denote the number of observations with a value less than or equal to 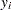, where is an indicator function. Let 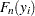denote the EDF estimate that is computed by using the method specified in the EMPIRICALCDF= option. Let 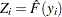denote the estimate of the CDF. Let denote the EDF estimate of 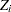values that are computed using the same method that is used to compute the EDF of 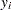values. Using the probability integral transformation, if is the true distribution of the random variable 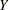, then the random variable 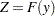is uniformly distributed between 0 and 1 (D’Agostino and Stephens 1986, Ch. 4). Thus, comparing 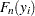with 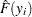is equivalent to comparing with 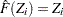(uniform distribution).

Note the following two points regarding which CDF estimates are used for computing the test statistics:

• If regressor variables are specified, then the CDF estimates 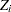used for computing the EDF test statistics are from a mixture distribution. See the section CDF and PDF Estimates with Regression Effects for details.

• If left-truncation is specified without the probability of observability and the method for computing the EDF estimate is KAPLANMEIER or MODIFIEDKM, then 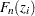is a conditional estimate of the EDF, as noted in the section EDF Estimates and Left-Truncation. However, 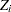is an unconditional estimate of the CDF. So, a conditional estimate of the CDF needs to be used for computing the EDF-based statistics. It is denoted by 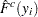and defined as: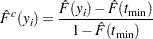

  where 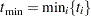is the smallest value of the left-truncation threshold.

  Note that if regressors are specified, then both 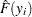and 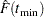are computed from a mixture distribution, as indicated previously.

In the following, it is assumed that 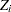denotes an appropriate estimate of the CDF if left-truncation or regression effects are specified.

Given this, the EDF-based statistics of fit are defined as follows:

KS

The Kolmogorov-Smirnov (KS) statistic computes the largest vertical distance between the CDF and the EDF. It is formally defined as follows:

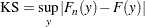
If the STANDARD method is used to compute the EDF, then the following formula is used:

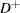
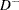
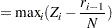
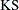
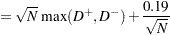
Note that 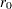is assumed to be 0.

If the method used to compute the EDF is any method other than the STANDARD method, then the following formula is used:

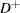
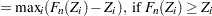
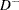
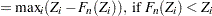
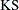
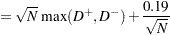
AD

The Anderson-Darling (AD) statistic is a quadratic EDF statistic that is proportional to the expected value of the weighted squared difference between the EDF and CDF. It is formally defined as follows:

If the STANDARD method is used to compute the EDF, then the following formula is used:

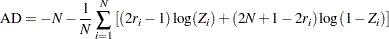
If the method used to compute the EDF is any method other than the STANDARD method, then the statistic can be computed by using the following two pieces of information:

• The EDF estimate is a step function. In the interval 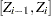, it is equal to .

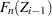• Using the probability integral transform 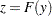, the formula simplifies to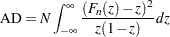

The computation formula can then be derived from the following approximation:

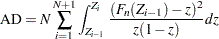
Assuming 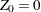, , 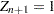, 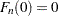and 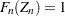yields the following computation formula:

where 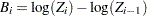and .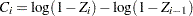

CvM

The Cramér-von-Mises (CvM) statistic is a quadratic EDF statistic that is proportional to the expected value of the squared difference between the EDF and CDF. It is formally defined as follows:

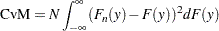
If the STANDARD method is used to compute the EDF, then the following formula is used:

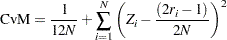
If the method used to compute the EDF is any method other than the STANDARD method, then the statistic can be computed by using the following two pieces of information:

• The EDF estimate is a step function. In the interval 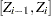, it is equal to .

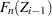• Using the probability integral transform 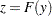, the formula simplifies to: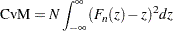

The computation formula can then be derived from the following approximation:

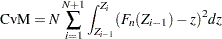
Assuming 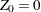, , 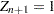and 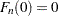yields the following computation formula: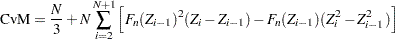

This formula is similar to the one proposed by Koziol and Green (1976).