| The SEVERITY Procedure |
| Empirical Distribution Function Estimation Methods |
The empirical distribution function (EDF) is a nonparametric estimate of the cumulative distribution function (CDF) of the distribution. PROC SEVERITY uses EDF estimates for computing the EDF-based statistics in addition to providing a nonparametric estimate of the CDF to the PARMINIT subroutine.
Let there be a set of 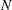 observations, each containing a triplet of values
observations, each containing a triplet of values 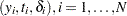 , where
, where 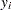 is the value of the response variable,
is the value of the response variable, 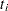 is the value of the left-truncation threshold, and
is the value of the left-truncation threshold, and 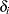 is the indicator of right-censoring. A missing value for
is the indicator of right-censoring. A missing value for 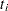 indicates no left-truncation.
indicates no left-truncation. 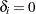 indicates a right-censored observation, in which case
indicates a right-censored observation, in which case 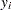 is assumed to record the right-censoring limit
is assumed to record the right-censoring limit 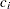 .
. 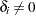 indicates an uncensored observation.
indicates an uncensored observation.
In the following definitions, an indicator function 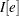 is used, which takes a value of 1 or 0 if the expression
is used, which takes a value of 1 or 0 if the expression  is true or false, respectively.
is true or false, respectively.
Given this notation, the EDF is estimated as follows:
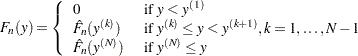 |
where 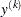 denotes the
denotes the 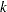 th order statistic of the set
th order statistic of the set  and
and  is the estimate computed at that value. The definition of
is the estimate computed at that value. The definition of 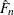 depends on the estimation method. You can specify a particular method or let PROC SEVERITY choose an appropriate method by using the EMPIRICALCDF= option in the MODEL statement. Each method computes
depends on the estimation method. You can specify a particular method or let PROC SEVERITY choose an appropriate method by using the EMPIRICALCDF= option in the MODEL statement. Each method computes 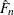 as follows:
as follows:
- STANDARD
This method is the standard way of computing EDF. The EDF estimate at observation
 is computed as follows:
is computed as follows: 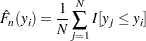
This method ignores any censoring and truncation information, even if it is specified. When no censoring or truncation information is specified, this is the default method chosen.
- KAPLANMEIER
This method is suitable primarily when left-truncation or right-censoring is specified. The Kaplan-Meier (KM) estimator, also known as the product-limit estimator, was first introduced by Kaplan and Meier (1958) for censored data. Lynden-Bell (1971) derived a similar estimator for left-truncated data. PROC SEVERITY uses the definition that combines both censoring and truncation information (Klein and Moeschberger 1997, Lai and Ying 1991).
The EDF estimate at observation
 is computed as
is computed as 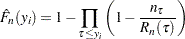
where
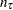 and
and 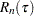 are defined as follows:
are defined as follows: 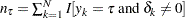 , which is the number of uncensored observations with response variable value equal to
, which is the number of uncensored observations with response variable value equal to  .
.  , which is the size (cardinality) of the risk set at
, which is the size (cardinality) of the risk set at  . The term risk set has its origins in survival analysis; it contains the events that are at the risk of failure at a given time,
. The term risk set has its origins in survival analysis; it contains the events that are at the risk of failure at a given time,  . In other words, it contains the events that have survived up to time
. In other words, it contains the events that have survived up to time  and might fail at or after
and might fail at or after  . For PROC SEVERITY, time is equivalent to the magnitude of the event and failure is equivalent to an uncensored and observable event, where observable means it satisfies the left-truncation threshold.
. For PROC SEVERITY, time is equivalent to the magnitude of the event and failure is equivalent to an uncensored and observable event, where observable means it satisfies the left-truncation threshold.
If you specify either right-censoring or left-truncation and do not explicitly specify a method of computing EDF, then this is the default method used.
- MODIFIEDKM
The product-limit estimator used by the KAPLANMEIER method does not work well if the risk set size becomes very small. This can happen for right-censored data towards the right tail, and for left-truncated data at the left tail and propagate to the entire range of data. This was demonstrated by Lai and Ying (1991). They proposed a modification to the estimator that ignores the effects due to small risk set sizes.
The EDF estimate at observation
 is computed as
is computed as 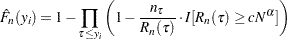
where the definitions of
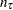 and
and 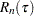 are identical to those used for the KAPLANMEIER method described previously.
are identical to those used for the KAPLANMEIER method described previously. You can specify the values of
 and
and  by using the C= and ALPHA= options. If you do not specify a value for
by using the C= and ALPHA= options. If you do not specify a value for  , the default value used is
, the default value used is 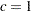 . If you do not specify a value for
. If you do not specify a value for  , the default value used is
, the default value used is  .
. As an alternative, you can also specify an absolute lower bound, say
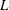 , on the risk set size by using the RSLB= option, in which case
, on the risk set size by using the RSLB= option, in which case 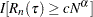 is replaced by
is replaced by  in the definition.
in the definition.
EDF Estimates and Left-Truncation
If left-truncation is specified without the probability of observability, the estimate  computed by KAPLANMEIER and MODIFIEDKM methods is a conditional estimate. In other words,
computed by KAPLANMEIER and MODIFIEDKM methods is a conditional estimate. In other words,  , where
, where 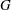 denotes the (unknown) distribution function of
denotes the (unknown) distribution function of 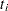 and
and  . In other words,
. In other words, 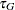 is the smallest threshold with a nonzero cumulative probability. For computational purposes, PROC SEVERITY computes
is the smallest threshold with a nonzero cumulative probability. For computational purposes, PROC SEVERITY computes 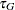 as
as  .
.
If left-truncation is specified with the probability of observability  , then PROC SEVERITY uses the additional information provided by
, then PROC SEVERITY uses the additional information provided by  to compute an unconditional estimate of the EDF. In particular, for each left-truncated observation
to compute an unconditional estimate of the EDF. In particular, for each left-truncated observation  with response variable value
with response variable value 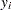 and truncation threshold
and truncation threshold 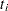 , an observation
, an observation 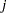 is added with weight
is added with weight 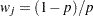 and
and  . Each added observation is assumed to be uncensored; that is,
. Each added observation is assumed to be uncensored; that is,  . Weight on each original observation
. Weight on each original observation  is assumed to be 1; that is,
is assumed to be 1; that is,  . Let
. Let 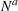 denote the number of observations in this appended set of observations. Then, the specified EDF method is used by assuming no left-truncation. For the KAPLANMEIER and MODIFIEDKM methods, definitions of
denote the number of observations in this appended set of observations. Then, the specified EDF method is used by assuming no left-truncation. For the KAPLANMEIER and MODIFIEDKM methods, definitions of 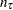 and
and 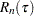 are modified to account for the weights on the observations.
are modified to account for the weights on the observations. 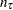 is now defined as
is now defined as 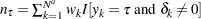 , and
, and 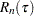 is defined as
is defined as  . From the definition of
. From the definition of 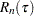 , note that each observation in the appended set is assumed to be observed; that is, the left-truncation information is not used, because it was used along with
, note that each observation in the appended set is assumed to be observed; that is, the left-truncation information is not used, because it was used along with  to add the observations. The estimate that is obtained using this method is an unconditional estimate of the EDF.
to add the observations. The estimate that is obtained using this method is an unconditional estimate of the EDF.
Note: This procedure is experimental.
Copyright © SAS Institute, Inc. All Rights Reserved.