| The SEVERITY Procedure |
| MODEL Statement |
- MODEL response-variable-name <( response-variable-options )> <= regressor-variable-list> </ fit-options> ;
This statement specifies the name of the response variable whose distribution needs to be modeled. You can also specify additional options to indicate any truncation or censoring of the response and any regression effects in this statement.
All the analysis variables specified in this statement must be present in the input data set that is specified by using the DATA= option in the PROC SEVERITY statement. The response variable and the regressor variables are expected to have nonmissing values. If any of the variables has a missing value in an observation, then a warning is written to the SAS log and that observation is ignored.
The following response-variable-options can be used in the MODEL statement:
- LEFTTRUNCATED | LT=variable-name <( left-truncation-options )>
- LEFTTRUNCATED | LT=number <( left-truncation-options )>
specifies the left-truncation variable or a global left-truncation threshold.
Using the first form, you can specify a data set variable that contains the left-truncation threshold. If the value of this variable is missing or 0 for some observations, then PROC SEVERITY assumes that such observations are not left-truncated.
Alternatively, using the second form, you can specify a left-truncation threshold that applies to all the observations in the data set. This threshold must be a nonzero positive number.
It is assumed that the response variable contains the observed values. By definition of left-truncation, you can observe only a value that is greater than the truncation threshold. If a response variable value is less than or equal to the threshold, a warning is printed to the SAS log, and the observation is ignored. More details about left-truncation are provided in the section Censoring and Truncation.
The following left-truncation option can be specified for an alternative interpretation of the left-truncation threshold:
- PROBOBSERVED | POBS=number
specifies the probability of observability, which is defined as the probability that the underlying severity event gets observed (and recorded) for the specified left-threshold value.
The specified number must lie in the (0.0, 1.0] interval. A value of 1.0 is equivalent to specifying that there is no left-truncation, because it means that no severity events can occur with a value less than or equal to the threshold. If you specify value of 1.0, PROC SEVERITY prints a warning to the SAS log and proceeds by assuming that LEFTTRUNCATED= option is not specified.
More details about the probability of observability are provided in the section Probability of Observability.
- RIGHTCENSORED | RC=variable-name <(number list)>
- RIGHTCENSORED | RC=number
specifies the right-censoring variable with indicator values, or a global right-censoring limit.
Using the first form, you can specify a data set variable that contains the censoring indicator values. By default, a value of 0 for the censor indicator variable indicates that the observed value of the response variable is censored on the right. In other words, the actual value is greater than or equal to the recorded value. You can optionally specify a list of censor indicator values. If the censor indicator variable has a missing value, then that observation is treated as uncensored.
Alternatively, using the second form, you can specify a limit value for right-censoring that applies to all the observations in the data set. If the response variable value recorded for an observation is greater than or equal to the specified limit, then that observation is assumed to be censored at the limit. Otherwise, the observation is assumed to be uncensored. More details about right-censoring are provided in the section Censoring and Truncation.
- CRITERION | CRITERIA | CRIT=criterion-option
specifies the model selection criterion.
If two or more models are specified for estimation, then the one with the best value for the selection criterion is chosen as the best model. If the OUTMODELINFO= data set is specified, then the best model’s observation has a value of 1 for the _SELECTED_ variable. You can specify one of the following criterion-options:
- LOGLIKELIHOOD | LL
specifies
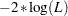 as the selection criterion, where
as the selection criterion, where 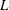 is the likelihood of the data. A lower value is deemed better. This is the default.
is the likelihood of the data. A lower value is deemed better. This is the default. - AIC
specifies the Akaike’s information criterion (AIC) as the selection criterion. A lower value is deemed better.
- AICC
specifies the finite-sample corrected Akaike’s information criterion (AICC) as the selection criterion. A lower value is deemed better.
- BIC
specifies Schwarz Bayesian information criterion (BIC) as the selection criterion. A lower value is deemed better.
- KS
specifies the Kolmogorov-Smirnov (KS) statistic value, which is computed by using the empirical distribution function (EDF) estimate, as the selection criterion. A lower value is deemed better.
- AD
specifies the Anderson-Darling (AD) statistic value, which is computed by using the empirical distribution function (EDF) estimate, as the selection criterion. A lower value is deemed better.
- CVM
specifies the Cra
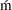 er-von-Mises (CvM) statistic value, which is computed by using the empirical distribution function (EDF) estimate, as the selection criterion. A lower value is deemed better.
er-von-Mises (CvM) statistic value, which is computed by using the empirical distribution function (EDF) estimate, as the selection criterion. A lower value is deemed better.
More details about these options are provided in the section Statistics of Fit.
- EMPIRICALCDF | EDF=method
specifies the method to use for computing the nonparametric or empirical estimate of the cumulative distribution function of the data. The following methods can be specified:
- AUTOMATIC | AUTO
specifies that the method be chosen automatically based on the data specification. This option is the default. If no right-censoring or left-truncation is specified, then the standard empirical estimation method (STANDARD) is chosen. If either right-censoring or left-truncation is specified, then the Kaplan-Meier method (KAPLANMEIER) is chosen.- STANDARD | STD
specifies that the standard empirical estimation method be used. This ignores any censoring or truncation information even if specified, and can thus result in estimates that are more biased than those obtained with other methods more suitable for such data.- KAPLANMEIER | KM
specifies that the product limit estimator proposed by Kaplan and Meier (1958) be used.- MODIFIEDKM | MKM <(options)>
specifies that the modified product limit estimator be used. This method allows the estimates to be more robust by ignoring the contributions to the estimate due to small risk-set sizes. The risk set is the set of observations at the risk of failing, where an observation is said to fail if it has not been processed yet and might experience censoring or truncation. The minimum risk-set size that makes it eligible to be included in the estimation can be specified either as an absolute lower bound on the size (RSLB= option) or a relative lower bound determined by the formula proposed by Lai and Ying (1991). Values of
proposed by Lai and Ying (1991). Values of  and
and  can be specified by using the C= and ALPHA= options respectively. By default, the relative lower bound is used with values of
can be specified by using the C= and ALPHA= options respectively. By default, the relative lower bound is used with values of 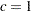 and
and  . However, you can modify the default by using the following options:
. However, you can modify the default by using the following options: - RSLB=number
specifies the absolute lower bound on the risk set size to be included in the estimate.
- C=number
specifies the value to use for
 when the lower bound on the risk set size is defined as
when the lower bound on the risk set size is defined as  . This value must satisfy
. This value must satisfy 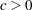 .
. - ALPHA | A=number
specifies the value to use for
 when the lower bound on the risk set size is defined as
when the lower bound on the risk set size is defined as  . This value must satisfy
. This value must satisfy 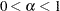 .
.
More details about each of the methods are provided in the section Empirical Distribution Function Estimation Methods.
Note: This procedure is experimental.
Copyright © SAS Institute, Inc. All Rights Reserved.