| The SEVERITY Procedure |
| Parameter Estimation Method |
PROC SEVERITY uses the maximum likelihood (ML) method to estimate the parameters of each model. A nonlinear optimization process is used to maximize the log of the likelihood function.
Likelihood Function
Let 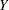 denote the random response variable, and let
denote the random response variable, and let 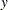 denote its value recorded in an observation in the input data set. Let
denote its value recorded in an observation in the input data set. Let 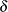 denote the censoring indicator:
denote the censoring indicator: 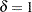 indicates that the observation is uncensored (sometimes referred to as an event observation) and
indicates that the observation is uncensored (sometimes referred to as an event observation) and 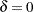 indicates that the observation is right-censored. When
indicates that the observation is right-censored. When 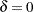 , the recorded value of
, the recorded value of  is assumed to be the censoring limit, denoted by
is assumed to be the censoring limit, denoted by  . Let
. Let  denote the left-truncation threshold. Let
denote the left-truncation threshold. Let 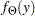 and
and 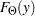 denote the PDF and CDF respectively, evaluated at
denote the PDF and CDF respectively, evaluated at 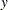 for a set of parameter values
for a set of parameter values  . Then, the set of input observations can be categorized into the following four subsets within each BY group:
. Then, the set of input observations can be categorized into the following four subsets within each BY group:
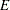 : the set of uncensored observations that are not left-truncated. The likelihood of an observation
: the set of uncensored observations that are not left-truncated. The likelihood of an observation  is
is 
 : the set of uncensored observations that are left-truncated. The likelihood of an observation
: the set of uncensored observations that are left-truncated. The likelihood of an observation  is
is 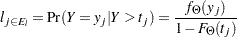
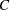 : the set of right-censored observations that are not left-truncated. The likelihood of an observation
: the set of right-censored observations that are not left-truncated. The likelihood of an observation 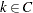 is
is 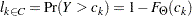
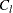 : the set of right-censored observations that are left-truncated. The likelihood of an observation
: the set of right-censored observations that are left-truncated. The likelihood of an observation 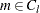 is
is 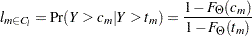
Note that 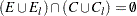 . Also, the sets
. Also, the sets  and
and 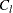 are empty when left-truncation is not specified, and the sets
are empty when left-truncation is not specified, and the sets 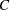 and
and 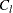 are empty when right-censoring is not specified.
are empty when right-censoring is not specified.
Given this, the likelihood of the data 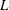 is as follows:
is as follows:
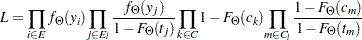 |
The maximum likelihood procedure used by PROC SEVERITY finds an optimal set of parameter values 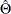 that maximizes
that maximizes 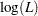 subject to the boundary constraints on parameter values. Note that for a distribution dist, such boundary constraints can be specified by using the dist_LOWERBOUNDS and dist_UPPERBOUNDS subroutines. Some aspects of the optimization process can be controlled by using the NLOPTIONS statement.
subject to the boundary constraints on parameter values. Note that for a distribution dist, such boundary constraints can be specified by using the dist_LOWERBOUNDS and dist_UPPERBOUNDS subroutines. Some aspects of the optimization process can be controlled by using the NLOPTIONS statement.
Probability of Observability and Likelihood
If probability of observability is specified for the left-truncation, then PROC SEVERITY uses a modified likelihood function for each truncated observation. If the probability of observability is 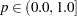 , then for each left-truncated observation with truncation threshold
, then for each left-truncated observation with truncation threshold  , there exist
, there exist 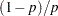 observations with a response variable value less than or equal to
observations with a response variable value less than or equal to  . Each such observation has a probability of
. Each such observation has a probability of 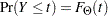 . Thus, following the notation of the section Likelihood Function, the likelihood of the data is as follows:
. Thus, following the notation of the section Likelihood Function, the likelihood of the data is as follows:
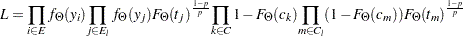 |
Note that the likelihood of the observations that are not left-truncated (observations in sets 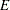 and
and 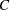 ) is not affected.
) is not affected.
Estimating Covariance and Standard Errors
PROC SEVERITY computes an estimate of the covariance matrix of the parameters by using the asymptotic theory of the maximum likelihood estimators (MLE). If 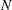 denotes the number of observations used for estimating a parameter vector
denotes the number of observations used for estimating a parameter vector 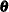 , then the theory states that as
, then the theory states that as  , the distribution of
, the distribution of 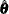 , the estimate of
, the estimate of 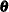 , converges to a normal distribution with mean
, converges to a normal distribution with mean 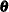 and covariance
and covariance  such that
such that 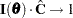 , where
, where 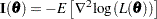 is the information matrix for the likelihood of the data,
is the information matrix for the likelihood of the data, 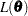 . The covariance estimate is obtained by using the inverse of the information matrix.
. The covariance estimate is obtained by using the inverse of the information matrix.
In particular, if 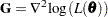 denotes the Hessian matrix of the log likelihood, then the covariance estimate is computed as
denotes the Hessian matrix of the log likelihood, then the covariance estimate is computed as
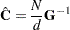 |
where 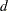 is a denominator determined by the VARDEF= option. If VARDEF=N, then
is a denominator determined by the VARDEF= option. If VARDEF=N, then 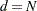 , which yields the asymptotic covariance estimate. If VARDEF=DF, then
, which yields the asymptotic covariance estimate. If VARDEF=DF, then 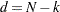 , where
, where 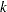 is number of parameters (the model’s degrees of freedom). The VARDEF=DF option is the default, because it attempts to correct the potential bias introduced by the finite sample.
is number of parameters (the model’s degrees of freedom). The VARDEF=DF option is the default, because it attempts to correct the potential bias introduced by the finite sample.
The standard error  of the parameter
of the parameter 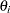 is computed as the square root of the
is computed as the square root of the  th diagonal element of the estimated covariance matrix; that is,
th diagonal element of the estimated covariance matrix; that is,  .
.
Note that covariance and standard error estimates might not be available if the Hessian matrix is found to be singular at the end of the optimization process. This can especially happen if the optimization process stops without converging.
Note: This procedure is experimental.
Copyright © SAS Institute, Inc. All Rights Reserved.