| The SEVERITY Procedure |
| Estimating Regression Effects |
The SEVERITY procedure enables you to estimate the effects of regressor (exogenous) variables while fitting a distribution model if the distribution has a scale parameter or a log-transformed scale parameter.
Let  (
(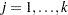 ) denote the
) denote the 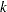 regressor variables. Let
regressor variables. Let 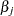 denote the regression parameter that corresponds to the regressor
denote the regression parameter that corresponds to the regressor  . If regression effects are not specified, then the model for the response variable
. If regression effects are not specified, then the model for the response variable 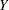 is of the form
is of the form
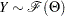 |
where 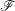 is the distribution of
is the distribution of 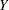 with parameters
with parameters 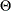 . This model is typically referred to as the error model. The regression effects are modeled by extending the error model to the following form:
. This model is typically referred to as the error model. The regression effects are modeled by extending the error model to the following form:
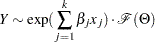 |
Under this model, the distribution of 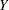 is valid and belongs to the same parametric family as
is valid and belongs to the same parametric family as 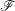 if and only if
if and only if 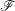 has a scale parameter. Let
has a scale parameter. Let 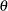 denote the scale parameter and
denote the scale parameter and 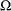 denote the set of nonscale distribution parameters of
denote the set of nonscale distribution parameters of 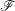 . Then the model can be rewritten as
. Then the model can be rewritten as
 |
such that 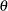 is affected by the regressors as
is affected by the regressors as
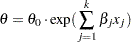 |
where 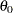 is the base value of the scale parameter. Thus, the regression model consists of the following parameters:
is the base value of the scale parameter. Thus, the regression model consists of the following parameters: 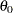 ,
, 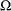 , and
, and  .
.
Given this form of the model, distributions without a scale parameter cannot be considered when regression effects are to be modeled. If a distribution does not have a direct scale parameter, then PROC SEVERITY accepts it only if it has a log-transformed scale parameter — that is, if it has a parameter 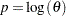 . You must define the SCALETRANSFORM function to specify the log-transformation when you define the distribution model.
. You must define the SCALETRANSFORM function to specify the log-transformation when you define the distribution model.
Parameter Initialization for Regression Models
Let a random variable 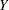 be distributed as
be distributed as 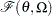 , where
, where 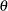 is the scale parameter. By definition of the scale parameter, a random variable
is the scale parameter. By definition of the scale parameter, a random variable 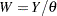 is distributed as
is distributed as  such that
such that 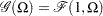 . Given a random error term
. Given a random error term  that is generated from a distribution
that is generated from a distribution  , a value
, a value 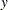 from the distribution of
from the distribution of 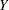 can be generated as
can be generated as
 |
Taking the logarithm of both sides and using the relationship of 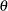 with the regressors yields:
with the regressors yields:
 |
If you do not provide initial values for the regression and distribution parameters, then PROC SEVERITY makes use of the preceding relationship to initialize parameters of a regression model with distribution dist as follows:
The following linear regression problem is solved to obtain initial estimates of
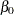 and
and 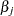 :
: 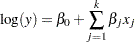
The estimates of
 in the solution of this regression problem are used to initialize the respective regression parameters of the model.
in the solution of this regression problem are used to initialize the respective regression parameters of the model. The results of this regression are also used to detect whether any regressors are linearly dependent on the other regressors. If any such regressors are found, then a warning is written to the SAS log and the corresponding regressor is eliminated from further analysis. The estimates for linearly dependent regressors are denoted by a special missing value of .R in the OUTEST= data set and in any displayed output.
Each input value
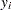 of the response variable is transformed to its scale-normalized version
of the response variable is transformed to its scale-normalized version 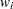 as
as 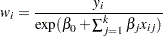
where
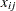 denotes the value of
denotes the value of 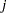 th regressor in the
th regressor in the  th input observation. These
th input observation. These 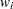 values are used to compute the input arguments for the dist_PARMINIT subroutine. The values that are computed by the subroutine for nonscale parameters are used as their respective initial values. Let
values are used to compute the input arguments for the dist_PARMINIT subroutine. The values that are computed by the subroutine for nonscale parameters are used as their respective initial values. Let 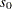 denote the value of the scale parameter that is computed by the subroutine. If the distribution has a log-transformed scale parameter
denote the value of the scale parameter that is computed by the subroutine. If the distribution has a log-transformed scale parameter 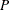 , then
, then 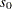 is computed as
is computed as 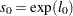 , where
, where  is the value of
is the value of 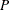 computed by the subroutine.
computed by the subroutine. The value of
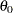 is initialized as
is initialized as 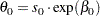
If you provide initial values for the regression parameters, then you must provide valid, nonmissing initial values for 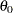 and
and 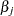 parameters.
parameters.
You can use only the INEST= data set to specify the initial values for 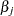 . You can use the .R special missing value to denote redundant regressors if any such regressors are specified in the MODEL statement.
. You can use the .R special missing value to denote redundant regressors if any such regressors are specified in the MODEL statement.
Initial values for 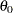 and other distribution parameters can be specified using either the INEST= data set or the INIT= option in the DIST statement. If the distribution has a direct scale parameter (no transformation), then the initial value for the first parameter of the distribution is used as an initial value for
and other distribution parameters can be specified using either the INEST= data set or the INIT= option in the DIST statement. If the distribution has a direct scale parameter (no transformation), then the initial value for the first parameter of the distribution is used as an initial value for 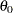 . If the distribution has a log-transformed scale parameter, then the initial value for the first parameter of the distribution is used as an initial value for
. If the distribution has a log-transformed scale parameter, then the initial value for the first parameter of the distribution is used as an initial value for 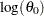 .
.
Reporting Estimates of Regression Parameters
When you request estimates to be written to the output (either ODS displayed output or in the OUTEST= data set), the estimate of the base value of the first distribution parameter is reported. If the first parameter is the log-transformed scale parameter, then the estimate of 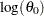 is reported; otherwise, the estimate of
is reported; otherwise, the estimate of 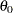 is reported. The transform of the first parameter of a distribution dist is controlled by the dist_SCALETRANSFORM function that is defined for it.
is reported. The transform of the first parameter of a distribution dist is controlled by the dist_SCALETRANSFORM function that is defined for it.
CDF and PDF Estimates with Regression Effects
When regression effects are estimated, the estimate of the scale parameter depends on the values of the regressors and estimates of the regression parameters. This results in a potentially different distribution for each observation. In order to make estimates of the cumulative distribution function (CDF) and probability density function (PDF) comparable across distributions and comparable to the empirical distribution function (EDF), PROC SEVERITY reports the CDF and PDF estimates from a mixture distribution. This mixture distribution is an equally weighted mixture of 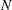 distributions, where
distributions, where 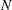 is the number of observations used for estimation. Each component of the mixture differs only in the value of the scale parameter.
is the number of observations used for estimation. Each component of the mixture differs only in the value of the scale parameter.
In particular, let  and
and 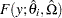 denote the PDF and CDF, respectively, of the component distribution due to observation
denote the PDF and CDF, respectively, of the component distribution due to observation  , where
, where 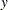 denotes the value of the response variable,
denotes the value of the response variable, 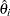 denotes the estimate of the scale parameter due to observation
denotes the estimate of the scale parameter due to observation  , and
, and 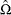 denotes the set of estimates of all other parameters of the distribution. The value of
denotes the set of estimates of all other parameters of the distribution. The value of 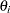 is computed as
is computed as
 |
where 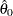 is an estimate of the base value of the scale parameter,
is an estimate of the base value of the scale parameter, 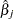 are the estimates of regression coefficients, and
are the estimates of regression coefficients, and 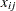 is the value of regressor
is the value of regressor 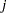 in observation
in observation  . Then, the PDF and CDF estimates,
. Then, the PDF and CDF estimates, 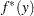 and
and 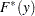 , respectively, of the mixture distribution at
, respectively, of the mixture distribution at 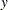 are computed as follows:
are computed as follows:
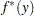 |
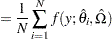 |
|||
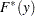 |
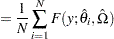 |
The CDF estimates reported in OUTCDF= data set and plotted in CDF plots are the 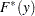 values. The PDF estimates plotted in PDF plots are the
values. The PDF estimates plotted in PDF plots are the 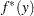 values.
values.
If left-truncation is specified without the probability of observability, then the conditional CDF estimate from the mixture distribution is computed as follows: Let 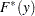 denote an unconditional mixture estimate of the CDF at
denote an unconditional mixture estimate of the CDF at 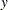 and
and  be the smallest value of the left-truncation threshold. Let
be the smallest value of the left-truncation threshold. Let  denote an unconditional mixture estimate of the CDF at
denote an unconditional mixture estimate of the CDF at  . Then, the conditional mixture estimate of the CDF at
. Then, the conditional mixture estimate of the CDF at 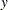 is computed as
is computed as 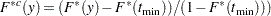 .
.
Note: This procedure is experimental.
Copyright © SAS Institute, Inc. All Rights Reserved.