| The SEVERITY Procedure |
| Predefined Utility Functions |
The following predefined utility functions are provided with the SEVERITY procedure and are available in the SASHELP.SVRTDIST library:
- SVRTUTIL_HILLCUTOFF:
This function computes an estimate of the value where the right tail of a distribution is expected to begin. The function implements the algorithm described in Danielsson et al. 2001. The description of the algorithm uses the following notation:
number of observations in the original sample
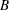
number of bootstrap samples to draw
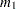
size of the bootstrap sample in the first step of the algorithm (
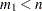 )
) 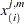
 th order statistic of
th order statistic of 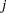 th bootstrap sample of size
th bootstrap sample of size  (
( )
) 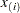
 th order statistic of the original sample (
th order statistic of the original sample (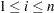 )
)
Given the input sample
 and values of
and values of 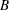 and
and 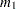 , the steps of the algorithm are as follows:
, the steps of the algorithm are as follows: Take
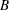 bootstrap samples of size
bootstrap samples of size 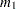 from the original sample.
from the original sample. Find the integer
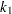 that minimizes the bootstrap estimate of the mean squared error:
that minimizes the bootstrap estimate of the mean squared error: 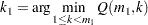
Take
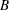 bootstrap samples of size
bootstrap samples of size 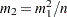 from the original sample.
from the original sample. Find the integer
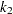 that minimizes the bootstrap estimate of the mean squared error:
that minimizes the bootstrap estimate of the mean squared error: 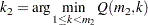
Compute the integer
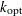 , which is used for computing the cutoff point:
, which is used for computing the cutoff point: 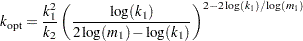
Set the cutoff point equal to
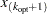 .
.
The bootstrap estimate of the mean squared error is computed as

The mean squared error of
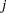 th bootstrap sample is computed as
th bootstrap sample is computed as 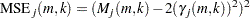
where
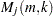 is a control variate proposed by Danielsson et al. 2001,
is a control variate proposed by Danielsson et al. 2001, 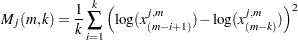
and
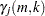 is the Hill’s estimator of the tail index (Hill 1975),
is the Hill’s estimator of the tail index (Hill 1975), 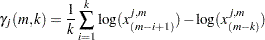
This algorithm has two tuning parameters,
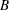 and
and 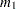 . The number of bootstrap samples
. The number of bootstrap samples 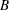 is chosen based on the availability of computational resources. The optimal value of
is chosen based on the availability of computational resources. The optimal value of 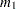 is chosen such that the following ratio,
is chosen such that the following ratio,  , is minimized:
, is minimized: 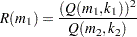
The SVRTUTIL_HILLCUTOFF utility function implements the preceding algorithm. It uses the grid search method to compute the optimal value of
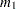 .
. Type: Function
Signature: SVRTUTIL_HILLCUTOFF(n, x{*}, b, s, status)
Argument Description:
- n
Dimension of the array x.
- x{*}
Input numeric array of dimension
 that contains the sample.
that contains the sample. - b
Number of bootstrap samples used to estimate the mean squared error. If b is less than 10, then a default value of 50 is used.
- s
Approximate number of steps used to search the optimal value of
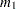 in the range
in the range 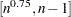 . If s is less than or equal to 1, then a default value of 10 is used.
. If s is less than or equal to 1, then a default value of 10 is used. - status
Output argument that contains the status of the algorithm. If the algorithm succeeds in computing a valid cutoff point, then status is set to 0. If the algorithm fails, then status is set to 1.
Return value: The cutoff value where the right tail is estimated to start. If the size of the input sample is inadequate (
 ), then a missing value is returned and status is set to a missing value. If the algorithm fails to estimate a valid cutoff value (status = 1), then the fifth largest value in the input sample is returned.
), then a missing value is returned and status is set to a missing value. If the algorithm fails to estimate a valid cutoff value (status = 1), then the fifth largest value in the input sample is returned.
- SVRTUTIL_PERCENTILE:
This function computes the specified percentile given the EDF estimates of a sample. Let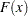 denote the EDF estimate at
denote the EDF estimate at  . Let
. Let 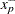 and
and 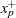 denote two consecutive values in the sample of
denote two consecutive values in the sample of  values such that
values such that 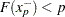 and
and 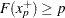 . Then, the function computes the 100
. Then, the function computes the 100 th percentile
th percentile 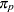 as
as 
where
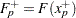 and
and 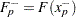 .
. Type: Function
Signature: SVRTUTIL_PERCENTILE(p, n, x{*}, F{*})
Argument Description:
- p
Desired percentile. The value must be in the interval (0,1). The function returns the 100
 th percentile.
th percentile. - n
Dimension of the x and F input arrays.
- x{*}
Input numeric array of dimension n that contains distinct values of the random variable observed in the sample. These values must be sorted in increasing order.
- F{*}
Input numeric array of dimension n in which each F[
 ] contains the EDF estimate for x[
] contains the EDF estimate for x[ ]. These values must be sorted in nondecreasing order.
]. These values must be sorted in nondecreasing order.
Return value: The 100
 th percentile of the input sample.
th percentile of the input sample.
- SVRTUTIL_RAWMOMENTS:
This subroutine computes the raw moments of a sample.Type: Subroutine
Signature: SVRTUTIL_RAWMOMENTS(n, x{*}, nx{*}, nRaw, raw{*})
Argument Description:
- n
Dimension of the x and nx input arrays.
- x{*}
Input numeric array of dimension n that contains distinct values of the random variable that are observed in the sample.
- nx{*}
Input numeric array of dimension n in which each nx[
 ] contains the number of observations in the sample that have the value x[
] contains the number of observations in the sample that have the value x[ ].
]. - nRaw
Desired number of raw moments. The output array raw contains the first nRaw raw moments.
- raw{*}
Output array of raw moments. The
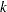 th element in the array (raw{
th element in the array (raw{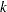 }) contains the
}) contains the 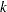 th raw moment, where
th raw moment, where 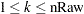 .
.
Return value: Numeric array raw that contains the first nRaw raw moments. The array contains missing values if the sample has no observations (that is, if all the values in the nx array add up to zero).
- SVRTUTIL_SORT:
This function sorts the given array of numeric values in an ascending or descending order.Type: Subroutine
Signature: SVRTUTIL_SORT(n, x{*}, flag)
Argument Description:
- n
Dimension of the input array x.
- x{*}
Numeric array that contains the values to be sorted at input. The subroutine uses the same array to return the sorted values.
- flag
A numeric value that controls the sort order. If flag is 0, then the values are sorted in an ascending order. If flag has any value other than 0, then the values are sorted in descending order.
Return value: Numeric array x, which is sorted in place (that is, the sorted array is stored in the same storage area occupied by the input array x).
Note: This procedure is experimental.
Copyright © SAS Institute, Inc. All Rights Reserved.